题目内容
已知点A(-1,y1)、B(-
,y2)、C(-2,y3)在y=(m2+1)x2上,则y1、y2、y3大小关系是 .
| 2 |
考点:二次函数图象上点的坐标特征
专题:
分析:先确定抛物线开口向上,对称轴为y轴,根据二次函数的增减性:在对称轴的左侧,y随x的增大而减小,由此确定y1、y2、y3的大小关系.
解答:解:y=(m2+1)x2,
∵m2+1>0,
∴抛物线开口向下,对称轴为y轴,
∵点A(-1,y1)、B(-
,y2)、C(-2,y3)在y=(m2+1)x2上,-1>-
>-2,
∴y1<y2<y3.
故答案为y1<y2<y3.
∵m2+1>0,
∴抛物线开口向下,对称轴为y轴,
∵点A(-1,y1)、B(-
| 2 |
| 2 |
∴y1<y2<y3.
故答案为y1<y2<y3.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.

练习册系列答案
相关题目
要使3x3+mx2+nx+42能被x2-5x+6整除,m、n应取的值为( )
| A、m=8、n=17 |
| B、m=-8、n=17 |
| C、m=8、n=-17 |
| D、m=-8、n=-17 |
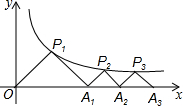 如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=