��Ŀ����
��ͼ��ֱ��l1��y1=﹣x+2��x�ᣬy��ֱ���A��B���㣬��P��m��3��Ϊֱ��l1��һ�㣬��һֱ��l2��y2=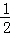 x+b����P��
x+b����P��
��1�����P�����b��ֵ��
��2������C��ֱ��l2��x��Ľ��㣬����Q�ӵ�C��ʼ��ÿ��1����λ���ٶ���x���������ƶ������Q���˶�ʱ��Ϊt�룮
����д������Q���˶������У���APQ�����S��t�ĺ�����ϵʽ��
�����tΪ����ʱ����APQ�����С��3��
���Ƿ����t��ֵ��ʹ��APQΪ���������Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
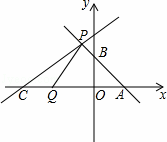
�⣻��1���ߵ�P��m��3��Ϊֱ��l1��һ�㣬
��3=﹣m+2�����m=﹣1��
���P������Ϊ��﹣1��3����
�ѵ�P���������y2= x+b�ã�3=
x+b�ã�3= ����﹣1��+b��
����﹣1��+b��
���b= ��
��
��2����b= ��
��
��ֱ��l2�Ľ���ʽΪy= x+
x+ ��
��
��C�������Ϊ��﹣7��0����
����ֱ��l1��y1=﹣x+2��֪A��2��0����
�൱Q��A��C֮��ʱ��AQ=2+7﹣t=9﹣t��
��S= AQ•|yP|=
AQ•|yP|= ����9﹣t����3=
����9﹣t����3= ﹣
﹣ t��
t��
��Q��A���ұ�ʱ��AQ=t﹣9��
��S= AQ•|yP|=
AQ•|yP|= ����t﹣9����3=
����t﹣9����3= t﹣
t﹣ ��
��
����APQ�����S��t�ĺ�����ϵʽΪS=﹣ t+
t+ ��S=
��S= t﹣
t﹣ ��
��
�ڡ�S��3��
��﹣ t+
t+ ��3��
��3�� t﹣
t﹣ ��3
��3
���t��7��t��11��
�۴��ڣ�
��Q��t﹣7��0����
��PQ=PAʱ����t﹣7+1��2+��0﹣3��2=��2+ 1��2+��0﹣3��2
1��2+��0﹣3��2
�ࣨt﹣6��2=32�����t=3��t=9����ȥ����
��AQ=PAʱ����t﹣7﹣2��2=��2+1��2+��0﹣3��2
�ࣨt﹣9��2=18�����t=9+3 ��t=9﹣3
��t=9﹣3 ��
��
��PQ=AQʱ����t﹣7+1��2+��0﹣3��2=��t﹣7﹣2��2��
�ࣨt﹣6��2+9=��t﹣9��2�����t=6��
�ʵ�t��ֵΪ3��9+3 ��9﹣3
��9﹣3 ��6ʱ����APQΪ���������Σ�
��6ʱ����APQΪ���������Σ�

 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д� B�� m
B�� m C�� m
C�� m D�� m
D�� m
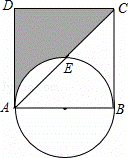
 ��A��B��C��D��ͬһ��Բ�ϣ���AD��BC���ӳ��߽��ڵ�E����ͼ�����������ι��У�������
��A��B��C��D��ͬһ��Բ�ϣ���AD��BC���ӳ��߽��ڵ�E����ͼ�����������ι��У�������
 2�� B�� 3�� C�� 4�� D�� 5��
2�� B�� 3�� C�� 4�� D�� 5��
 B��
B��  C��
C��  D��
D�� 
