题目内容
.一个等边三角形的边长为2,则这个等边三角形的面积为
 .
.
考点: 等边三角形的性质.
分析: 根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求三角形ABC的面积,即可解题.
解答: 解:∵等边三角形高线即中点,AB=2,
∴BD=CD=1,
在Rt△ABD中,AB=2,BD=1,
∴AD= =
= =
= ,
,
∴S△ABC= BC•AD=
BC•AD= ×2×
×2× =
= ,
,
故答案为: .
.


练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目

 B.
B.  C.
C.  D.
D. 

 有解,则a的取值范围是( )
有解,则a的取值范围是( )
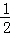 x+b过点P.
x+b过点P.