题目内容
18.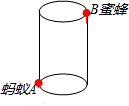 如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,
如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,(1)求蚂蚁从A到B处吃到蜂蜜最短距离;
(2)若蚂蚁刚出发时发现B处的蜂蜜正以每秒钟1cm沿杯内壁下滑,4秒钟后蚂蚁吃到了蜂蜜,求蚂蚁的平均速度至少是多少?
分析 (1)先将圆柱的侧面展开,再根据勾股定理求解即可;
(2)根据勾股定理得到蚂蚁所走的路程,于是得到结论.
解答  解:(1)如图所示,
解:(1)如图所示,
∵圆柱形玻璃容器,高12cm,底面周长为24cm,
∴AD=12cm,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{1{2}^{2}+1{2}^{2}}$=12$\sqrt{2}$(cm).
答:蚂蚁要吃到食物所走的最短路线长度是12$\sqrt{2}$cm;
(2)∵AD=12cm,
∴蚂蚁所走的路程=$\sqrt{1{2}^{2}+(12+4)^{2}}$=20,
∴蚂蚁的平均速度=20÷4=5(cm/s).
点评 本题考查的是平面展开-最短路径问题,将图形展开,利用勾股定理进行计算是解题的关键.

练习册系列答案
相关题目
10. 如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )
如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )
 如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )
如图,直线a、b被直线c、d所截,若∠1=∠2,∠3=115°,则∠4的度数为( )| A. | 55° | B. | 60° | C. | 65° | D. | 75° |
 小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )
小明在观察由一些相同小立方块搭成的几何体时,发现它的主视图、左视图、俯视图均为如图,则构成该几何体的小立方块的个数可能是( )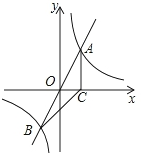 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
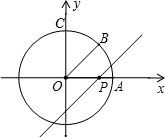 如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.
如图,⊙O是以数轴原点O为圆心,半径为3的圆,与坐标轴的正半轴分别交于A、C两点,OB平分∠AOC,点P在数轴上运动,过点P且与OB平行的直线与⊙O有公共点,则线段OP的取值范围是0<OP≤3$\sqrt{2}$.