题目内容
3.解下列不等式,并在数轴上表示其解集(1)5-x≤2x-4
(2)$\frac{1}{2}$(3y-1)-$\frac{1}{5}$y<y+1.
分析 (1)先移项,再合并得到-3x≤-9,然后把x的系数化为1即可得到不等式的解集,再利用数轴表示解集;
(2)先去分母、去括号、移项、合并得3y<15,然后把y的系数化为1即可得到不等式的解集,再利用数轴表示解集.
解答 解:(1)移项得-x-2x≤-4-5,
合并得-3x≤-9,
系数化为1得x≥3;
用数轴表示为:
(2)去分母得5(3y-1)-2y<10(y+1),
去括号得15y-5-2y<10y+10,
移项得15y-2y-10y<10+5,
合并得3y<15,
系数化为1得y<5,
用数轴表示为
点评 本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.也考查了用数轴表示不等式的解集.

练习册系列答案
相关题目
13.点P为直线l外一点,点A、B在直线l上,若PA=3,PB=5,则点P到直线l的距离为( )
| A. | 3 | B. | 小于3 | C. | 不大于3 | D. | 4 |
14.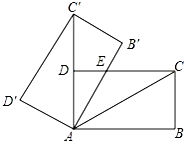 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )
 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )| A. | 12 | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
13.若分式方程$\frac{1}{x-1}$+3=$\frac{b-x}{a+x}$有增根,则a的值是( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
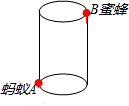 如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,
如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处, 如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°.
如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为75°. 如图,D、E是AB的三等分点,DF∥EG∥BC,则图中三部分面积S1:S2:S3=1:3:5.
如图,D、E是AB的三等分点,DF∥EG∥BC,则图中三部分面积S1:S2:S3=1:3:5.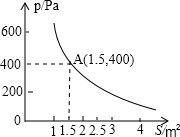 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.