题目内容
13.直线y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(1,2),写出这两个函数的表达式.分析 根据直线y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(1,2),将点A的横纵坐标分别代入两个函数解析式,可以求得k和b的值,从而可以写出两个函数的解析式,本题得以解决.
解答 解:∵点A(1,2)在反比例函数y=$\frac{k}{x}$的图象上,
∴$2=\frac{k}{1}$,
解得k=2,
即反比例函数的解析式为:y=$\frac{2}{x}$(x>0),
又∵直线y=x+b过点A(1,2),
∴2=1+b,
解得b=1,
即一次函数的解析式为:y=x+1,
由上可得,反比例函数的解析式为y=$\frac{2}{x}$(x>0),一次函数的解析式为y=x+1.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
4.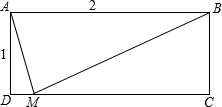 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{4}$ | C. | $\sqrt{3}-\frac{3}{2}$ | D. | $2-\sqrt{3}$ |
1.可以用来说明命题“若m<n,则$\frac{1}{m}$$>\frac{1}{n}$”是假命题的反例是( )
| A. | m=2,n=-3 | B. | m=-2,n=3 | C. | m=-2,n=-3 | D. | m=2,n=3 |
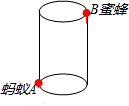 如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,
如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,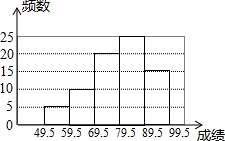 某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )
某校八年级(2)班数学单元测试全班所有学生成绩的频数分布直方图如图所示(满分100分,学生成绩取整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全部人数的( )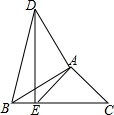 如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )
如图,在△ABC中,∠B=30°,∠C=45°,将△ABC绕点A顺时针旋转后得到△ADE(点B的对应点是点D,点C的对应点是点E),当点E在BC边上时,连接BD,则∠BDE的大小为( )