题目内容
9.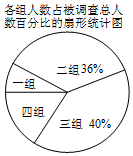 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:被调查同学每周课外阅读时间统计表.
| 组号 | 分组 | 频数 |
| 一 | 0≤x<2 | 4 |
| 二 | 2≤x<4 | 18 |
| 三 | 4≤x<6 | a |
| 四 | 6≤x<8 | 8 |
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
分析 (1)根据二组的人数和所占的百分比求出本次随机调查的学生数,再用总人数减去一、二、四组的人数,即可求出a的值,再用360°乘以第一组所占的百分比即可求出在扇形统计图中第一组对应的圆心角的度数;
(2)根据题意先画出树状图,得出所有情况数和选取的两名同学中恰好一名是男生,一名是女生的情况数,然后根据概率公式即可得出答案.
解答 解:(1)根据题意得:
$\frac{18}{36%}$=50(名)
答:本次随机调查学生共有50名,
a=50-4-18-8=20;
第一组对应的圆心角的度数是360°×$\frac{4}{50}$=28.8°;
故答案为:50,20,28.8;
(2)根据题意画树状图如下: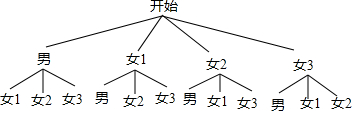
∵共有12种情况,选取的两名同学中恰好一名是男生,一名是女生的有6中情况,
∴选取的两名同学中恰好一名是男生,一名是女生的概率是$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查频率(数)分布表、扇形统计图以及画树状图法求概率,解题的关键是明确题意,利用数形结合的思想解答问题;概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
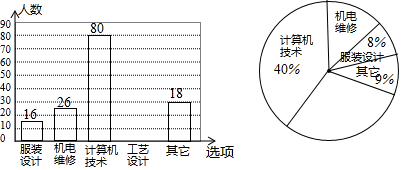
17. 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
请根据图表提供的信息,解答下列问题:
(1)表中的a=12,b=40;
(2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是108°;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,请用列表或画树状图的方法求正好抽到一名男同学和一名女同学的概率.
 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.| 分数段 (分数为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x<90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
(1)表中的a=12,b=40;
(2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是108°;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,请用列表或画树状图的方法求正好抽到一名男同学和一名女同学的概率.
1.我们知道:等腰三角形、平行四边形、菱形、双曲线、抛物线.这些都是我们在初中学习阶段学过的几何图形或函数的图象,那么从它们之中随机抽取两个,得到的都是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | 1 |
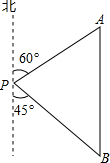 五一期间,小明到美丽的黄山参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)
五一期间,小明到美丽的黄山参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)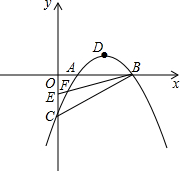 已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC
已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC 完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.
完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.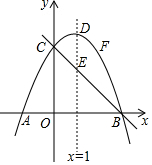 如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.
如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.