题目内容
20.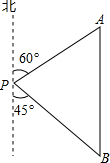 五一期间,小明到美丽的黄山参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)
五一期间,小明到美丽的黄山参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1米)
分析 由已知作PC⊥AB于C,可得△ABP中∠A=60°∠B=45°且PA=100m,要求AB的长,可以先求出AC和BC的长.
解答 解:由题意可知:作PC⊥AB于C,
∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△ACP中,
∵∠ACP=90°,∠APC=30°,
∴AC=$\frac{1}{2}$AP=50,PC=$\sqrt{3}$AC=50 $\sqrt{3}$.
在Rt△BPC中,
∵∠BCP=90°,∠BPC=45°,
∴BC=PC=50 $\sqrt{3}$.
∴AB=AC+BC=50+50 $\sqrt{3}$≈50+50×1.732≈136.6(米).
答:景点A与B之间的距离大约为136.6米
点评 本题考查了解直角三角形的应用,对于解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
9.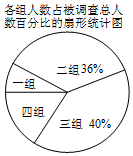 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
被调查同学每周课外阅读时间统计表.
(1)本次随机调查学生共有50名,表格中a的值为20,在扇形统计图中第一组对应的圆心角的度数是28.8度;
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:被调查同学每周课外阅读时间统计表.
| 组号 | 分组 | 频数 |
| 一 | 0≤x<2 | 4 |
| 二 | 2≤x<4 | 18 |
| 三 | 4≤x<6 | a |
| 四 | 6≤x<8 | 8 |
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
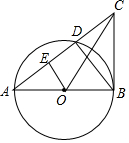 已知△ABC中,AB=8,BC=6,以AB为直径的⊙O与AC交于D点,连接BD,且BD=$\frac{24}{5}$.连接OC.
已知△ABC中,AB=8,BC=6,以AB为直径的⊙O与AC交于D点,连接BD,且BD=$\frac{24}{5}$.连接OC.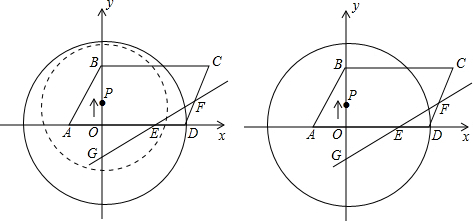
 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以20海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,我渔政船的航行路程是30$\sqrt{2}$海里.
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以20海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,我渔政船的航行路程是30$\sqrt{2}$海里. 如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.
如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.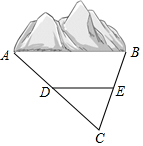 某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使点C均可直接到达A,B两点,测量找到AC和BC的中点D,E,测得DE的长为1200m,则隧道AB的长度为2400米.
某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使点C均可直接到达A,B两点,测量找到AC和BC的中点D,E,测得DE的长为1200m,则隧道AB的长度为2400米.