题目内容
19.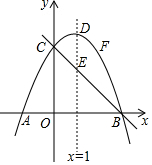 如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.
如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.(1)求抛物线的解析式.
(2)F为直线BC上方的抛物线上一个动点,是否存在点F,使四边形ABFC的面积为11?若存在,求出F点坐标;若不存在,说明理由.
(3)直线l∥DE,交BC于P点,交抛物线于Q点,当以D,E,P,Q为顶点的四边形是平行四边形时,直接写出P点坐标.
分析 (1)根据轴对称的性质,可得B点坐标,根据待定系数法,可得答案;
(2)根据平行于y的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得FG的长,根据面积可得关于m的方程,根据解方程,可得答案;
(3)根据平行于y的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得QP的长,根据平行四边形的对边相等,可得关于n的方程,根据解方程,可得答案.
解答 解:(1)由A,B关于x=1对称,得
B(4,0),
将A,B代入函数解析式,得
$\left\{\begin{array}{l}{4a-2b+4=0}\\{16a+4b+4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
抛物线的解析式为y=-$\frac{1}{2}$x2+x+4;
(2)F为直线BC上方的抛物线上一个动点,不存在点F,使四边形ABFC的面积为11,理由如下:
如图1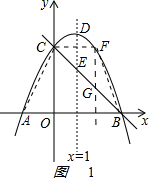 ,
,
当x=0时,y=4,即C(0,4).
AB的长是4-(-2)=6.
BC的解析式为y=-x+4
设F(m,-$\frac{1}{2}$m2+m+4),G(m,-m+4).
FG的长是(-$\frac{1}{2}$m2+m+4)-(-m+4)=-$\frac{1}{2}$m2+2m.
S四边形ABFC=S△ABC+SBCF
=$\frac{1}{2}$AB•OC+$\frac{1}{2}$FG•xB
=$\frac{1}{2}$×6×4+$\frac{1}{2}$×4(-$\frac{1}{2}$m2+2m),
由S四边形ABFC=11,得
$\frac{1}{2}$×6×4+$\frac{1}{2}$×4(-$\frac{1}{2}$m2+2m)=11,
化简,得m2-4m-1=0
解得m=2-$\sqrt{5}$<0(舍),m=2+$\sqrt{5}$>4(舍),
F为直线BC上方的抛物线上一个动点,不存在点F,使四边形ABFC的面积为11;
(3)如图2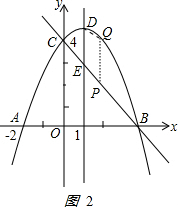
当x=1时,y=-$\frac{1}{2}$x2+x+4=$\frac{9}{2}$,即D(1,$\frac{9}{2}$),
BC的解析式为y=-x+4,
当x=1时y=3,即E(1,3),
DE的长为$\frac{9}{2}$-3=$\frac{3}{2}$
设Q(n,-$\frac{1}{2}$n2+n+4),P(n,-n+4).
PQ的长是(-$\frac{1}{2}$n2+n+4)-(-n+4)=-$\frac{1}{2}$n2+2n.
由DE=PQ,得
-$\frac{1}{2}$n2+2n=$\frac{3}{2}$,
化简,得
n2-4n+3=0,
解得n1=1(舍),n2=3,
-n+4=-3+4=1,
即P(3,1).
点评 本题考查了二次函数综合题,解(1)的关键是利用轴对称的性质得出B点坐标;解(2)的关键是利用面积的和差得出关于m的方程;解(3)的关键是利用平行四边形的对边相等得出关于n的方程.

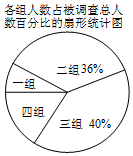 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:被调查同学每周课外阅读时间统计表.
| 组号 | 分组 | 频数 |
| 一 | 0≤x<2 | 4 |
| 二 | 2≤x<4 | 18 |
| 三 | 4≤x<6 | a |
| 四 | 6≤x<8 | 8 |
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
| 投篮次数n | 100 | 150 | 300 | 500 | 800 | 1000 |
| 投中次数m | 58 | 96 | 174 | 302 | 484 | 601 |
| 投中频率 | 0.580 | 0.640 | 0.580 | 0.604 | 0.605 | 0.601 |
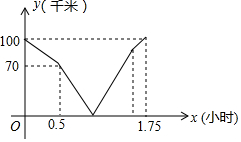 在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )| A. | 乙先出发的时间为0.5小时 | B. | 甲的速度是80千米/小时 | ||
| C. | 甲出发0.5小时后两车相遇 | D. | 甲到B地比乙到A地早$\frac{1}{12}$小时 |
| A. | 2x•3x=6x | B. | 3x-2x=x | C. | (2x)2=4x | D. | 6x÷2x=3x |
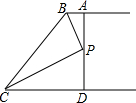 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是4.
如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是4. 如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.