题目内容
14.在2017年“KFC”乒乓球赛进校园活动中,某校甲、乙两队进行决赛,比赛规则规定:两队之间进行3局比赛,3局比赛必须全部打完,只要赢2局的队为获胜队,假如甲、乙两队之间每局比赛输赢的机会相同,且乙队已经赢得了第1局比赛.(1)列表或画树状图表示乙队所有比赛结果的可能性;
(2)求乙队获胜的概率.
分析 (1)画树状图展示所有4种等可能的结果数;
(2)找出乙队赢满两局的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有4种等可能的结果数;
(2)乙队赢满两局的结果数为3,
乙所以队获胜的概率=$\frac{3}{4}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.

练习册系列答案
相关题目
4.关于x的不等式x-m>0,恰有两个负整数解,则m的取值范围是( )
| A. | -3<m<-2 | B. | -3≤m<-2 | C. | -3≤m≤-2 | D. | -3<m≤-2 |
9.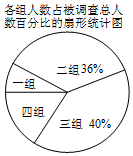 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
被调查同学每周课外阅读时间统计表.
(1)本次随机调查学生共有50名,表格中a的值为20,在扇形统计图中第一组对应的圆心角的度数是28.8度;
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:被调查同学每周课外阅读时间统计表.
| 组号 | 分组 | 频数 |
| 一 | 0≤x<2 | 4 |
| 二 | 2≤x<4 | 18 |
| 三 | 4≤x<6 | a |
| 四 | 6≤x<8 | 8 |
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
 如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.
如图,学校将一面积为240m2的矩形空地一边增加4m,另一边增加5m后,建成了一个正方形训练场,则此训练场的面积为400m2.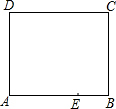 如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上的一点,AE=5,点P在长方形ABCD的一边上,要使△AEP是等腰三角形,则△AEP的底边长为5或5$\sqrt{2}$或4$\sqrt{5}$.
如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上的一点,AE=5,点P在长方形ABCD的一边上,要使△AEP是等腰三角形,则△AEP的底边长为5或5$\sqrt{2}$或4$\sqrt{5}$.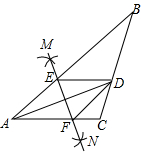 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则下列说法中正确的是( )
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:①分别以点A、D为圆心,以大于$\frac{1}{2}$AD的长为半径在AD两侧作弧,交于两点M、N;②连接MN分别交AB、AC于点E、F;③连接DE、DF.若BD=6,AF=4,CD=3,则下列说法中正确的是( )