题目内容

5．（1）解方程：2x2-3x=0；
（2）解不等式组：$\left\{\begin{array}{l}{x+8＜4x-1，①}\\{\frac{1}{2}x≤8-\frac{3}{2}x，②}\end{array}\right.$．

分析 （1）因式分解法求解可得；
（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．

解答 解：（1）∵x（2x-3）=0，
∴x=0或2x-3=0，
解得：x=0或x=$\frac{3}{2}$；

（2）解不等式①，得：x＞3，
解不等式②，得：x≤4，
则不等式组的解集为3＜x≤4．

点评 本题考查的是解一元二次方程和解一元一次不等式组，正确求出每一个不等式解集是基础，掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．

练习册系列答案
相关题目
15．某中学现要从两位男生和两位女生中，选派两位同学分别作为1号选手和2号选手代表学校参加汉字听写大赛．
（1）请用树形图或列表法列举出所有可能选派的结果；
（2）求恰好选派一男一女两位同学参赛的概率．
16．先化简，再求值：（$\frac{1}{b}$-$\frac{1}{a}$）÷$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$•$\frac{1}{2a+2b}$，其中a=$\sqrt{3}$+$\sqrt{2}$，b=$\sqrt{3}$-$\sqrt{2}$．
13．若反比例函数y=$\frac{k}{x}$的图象经过（3，4），则该函数的图象一定经过（　　）
A．（3，-4）B．（-4，-3）C．（-6，2）D．（4，4）
20．如图，AC、BD是菱形ABCD的对角线，若∠BAC=55°，则∠ADB等于35°．
10．某调查公司对本区域的共享单车数量及使用次数进行了调查发现，今年3月份第1周共有各类单车1000辆，第2周比第1周增加了10%，第3周比第2周增加了100辆，调查还发现某款单车深受群众喜爱，第1周该单车的每辆平均使用次数是这一周所有单车平均使用次数的2.5倍，第2、第3周该单车的每辆平均使用次数都比前一周增长一个相同的百分数m，第3周所有单车的每辆平均使用次数比第1周增加的百分数也是m，而且第3周该款单车（共100辆）的总使用次数占到所有单车总使用次数的四分之一．（注：总使用次数=每辆平均使用次数×车辆数）
（1）求第3周该区域内各类共享单车的数量；
（2）求m的值．
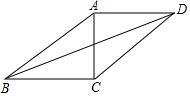17．在?ABCD中，对角线AC、BD交于点E，AC⊥BC，AB=8，∠ABC=30°，
（1）求BD的长．
（2）若点P从点B出发沿B-A-D的路线以2cm/s的速度向点D移动，同时点Q从点C出发沿C-D的路线以1cm/s的速度向点D移动，当一点到达C时，另一点也停止移动，当t取何值时，线段PQ将平行四边形ABCD的面积分为相等的两部分？
14．先化简分式：（$\frac{{a}^{2}-4}{{a}^{2}-4a+4}$$-\frac{2}{a-2}$）÷$\frac{{a}^{2}+2a}{a-2}$，再从不等式组$\left\{\begin{array}{l}{a+1＞0}\\{1-\frac{1}{2}a≥0}\end{array}\right.$的解集中选出合适的整数作为a的值，代入求值．
15．某校对九年级全体学生进行了一次学业水平测试，成绩评定分为A、B、C、D四个等级（A、B、C、D分别代表优秀、良好、合格、不合格）．该校从九年级学生中随机抽取了一部分学生的成绩，绘制成以下两幅不完整的统计图．请你根据统计图提供的信息解答下列问题；
（1）将下面的条形图补充完整，写出扇形统计图中等级C的百分比．
（2）若等级D的5名学生的成绩（单位：分）分别是55、48、57、51、55，求这5个数据中的中位数和众数．
（3）如果该校九年级共有500，试估计在这次测试中成绩达到优秀的人数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网