题目内容
计算:
(1)(
)-2-tan30°+|1-
|-(π-3.14)0;
(2)先化简,再求值:
÷(a+2-
),其中a满足a2+3a=5.
(1)(
| 1 |
| 2 |
| 3 |
(2)先化简,再求值:
| a-3 |
| 3a2-6a |
| 5 |
| a-2 |
考点:分式的化简求值,实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值
专题:
分析:(1)根据绝对值、负指数幂、特殊角的三角函数值、0指数幂的定义解答;
(2)将分式化简,然后整体代入求值即可.
(2)将分式化简,然后整体代入求值即可.
解答:解:(1)原式=
-
+
-1-1=4-
+
-2=2+
;
(2)原式=
÷[
-
]
=
÷
=
•
=
;
当a2+3a=5时,原式=
=
=
.
| 1 | ||
(
|
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
2
| ||
| 3 |
(2)原式=
| a-3 |
| 3a(a-2) |
| a2-4 |
| a-2 |
| 5 |
| a-2 |
=
| a-3 |
| 3a(a-2) |
| a2-9 |
| a-2 |
=
| a-3 |
| 3a(a-2) |
| a-2 |
| (a-3)(a+3) |
=
| 1 |
| 3a(a+3) |
当a2+3a=5时,原式=
| 1 |
| 3(a2+3a) |
| 1 |
| 3×5 |
| 1 |
| 15 |
点评:(1)本题考查了实数的运算,涉及乘方、负指数幂、特殊角的三角函数值、0指数幂等知识;
(2)本题考查了分式的化简求值,在代入求值时,要注意整体思想的应用.
(2)本题考查了分式的化简求值,在代入求值时,要注意整体思想的应用.

练习册系列答案
相关题目
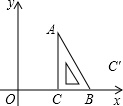 如图,把一块含有30°角的直角三角尺放置在平面直角坐标系中,BC边落在x轴的正半轴上,点A在第一限象内,∠ACB=90°,∠CAB=30°,AC=4
如图,把一块含有30°角的直角三角尺放置在平面直角坐标系中,BC边落在x轴的正半轴上,点A在第一限象内,∠ACB=90°,∠CAB=30°,AC=4 已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC.
已知点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连结BE交CD于点O,求证:△AOD≌△BOC.