题目内容
直角坐标系中,四边形ABCD的顶点坐标依次为A(-1,0),B(a,b),C(-1,5),D(c,d)
(1)当点D在y轴上,且四边形ABCD是菱形时,求点B的坐标;
(2)当四边形ABCD是菱形时,求a,b,c,d应满足的条件;
(3)四边形ABCD是正方形时,求a,c的值.
(1)当点D在y轴上,且四边形ABCD是菱形时,求点B的坐标;
(2)当四边形ABCD是菱形时,求a,b,c,d应满足的条件;
(3)四边形ABCD是正方形时,求a,c的值.
考点:菱形的性质,坐标与图形性质,正方形的性质
专题:
分析:(1)根据点A、C的横坐标判断出AC⊥x轴,再根据菱形的对角线互相垂直平分求出d,然后求出a、b,从而得解;
(2)根据菱形的对角线互相垂直平分可得AC⊥BD,AC的中点即为BD的中点,然后解答即可;
(3)根据正方形的对角线相等解答.
(2)根据菱形的对角线互相垂直平分可得AC⊥BD,AC的中点即为BD的中点,然后解答即可;
(3)根据正方形的对角线相等解答.
解答:解:(1)∵A(-1,0),(-1,5),
∴AC⊥x轴,且AC=5-0=5,
∵四边形ABCD是菱形,
∴AC垂直平分BD,
∵点D在y轴上,
∴b=d=
,
=-1,
解得a=-2,
∴点B(-2,
);
(2)∵四边形ABCD是菱形,
∴AC垂直平分BD,
∴
=-1,b=d,
整理得,a+c=-2,b=d;
(3)∵四边形ABCD是正方形,
∴BD=AC,
∴c-a=5,
又∵a+c=-2,
∴c=
,a=-
.
∴AC⊥x轴,且AC=5-0=5,
∵四边形ABCD是菱形,
∴AC垂直平分BD,
∵点D在y轴上,
∴b=d=
| 5 |
| 2 |
| a+0 |
| 2 |
解得a=-2,
∴点B(-2,
| 5 |
| 2 |
(2)∵四边形ABCD是菱形,
∴AC垂直平分BD,
∴
| a+c |
| 2 |
整理得,a+c=-2,b=d;
(3)∵四边形ABCD是正方形,
∴BD=AC,
∴c-a=5,
又∵a+c=-2,
∴c=
| 3 |
| 2 |
| 7 |
| 3 |
点评:本题考查了菱形的性质,坐标与图形性质,正方形的性质,主要利用了菱形的对角线互相垂直平分以及正方形和菱形的关系,判断出AC与x轴垂直是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 已知:如图,正方形ABCD,E,F分别为DC,BC中点.
已知:如图,正方形ABCD,E,F分别为DC,BC中点.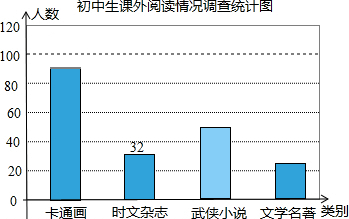 4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:
4月23日是“世界读书日”,今年世界读书日的主题是“阅读,让我们的世界更丰富”.某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题: 如图,已知△ABC中,以AB为直径的半⊙O交AC于D,交BC于E,BE=CE,∠C=70°,求∠DOE的度数.
如图,已知△ABC中,以AB为直径的半⊙O交AC于D,交BC于E,BE=CE,∠C=70°,求∠DOE的度数. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: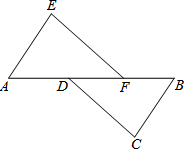 如图,A,D,F,B在同一直线上,AE=BC,且AE∥BC.添加一个条件
如图,A,D,F,B在同一直线上,AE=BC,且AE∥BC.添加一个条件