题目内容
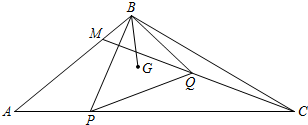
已知:如图,在△ABC中,AB=4,BC=5,点P在边AC上,且AP=
AB,联结BP,以BP为一边作△BPQ(点B、P、Q按逆时针排列),点G是△BPQ的重心,联结BG,∠PBG=∠BCA,∠QBG=∠BAC,联结CQ并延长,交边AB于点M.设PC=x,
=y.
(1)求
的值;
(2)求y关于x的函数关系式.
| 1 |
| 2 |
| MQ |
| MC |
(1)求
| BP |
| BQ |
(2)求y关于x的函数关系式.

考点:相似形综合题
专题:
分析:(1)延长BG,交边PQ于点D,延长BD至点E,使DE=BD,连接PE,先证出△PDE≌△QDB,得出PE=BQ,∠PED=∠QBD,再证出△BPE∽△CBA,得出
=
=
,即可证出
=
;
(2)延长AB至点F,使BF=AB,连接QF,过点Q作QH∥AC,交边AB于点H,证出
=
,再根据∠PBC=∠QBF,证出△PBC∽△QBF,得出∠BCP=∠BFQ,
=
=
,再根据
=
=
,得出
•
=(
)2,从而求出HQ=
PC=
x,最后根据
=
得出y=
,再进行整理即可.
| BP |
| PE |
| BC |
| AB |
| 5 |
| 4 |
| BP |
| BQ |
| 5 |
| 4 |
(2)延长AB至点F,使BF=AB,连接QF,过点Q作QH∥AC,交边AB于点H,证出
| BP |
| BQ |
| BC |
| BF |
| PC |
| QF |
| BP |
| BQ |
| 5 |
| 4 |
| QF |
| HQ |
| BC |
| AB |
| 5 |
| 4 |
| PC |
| QF |
| QF |
| HQ |
| 5 |
| 4 |
| 16 |
| 25 |
| 16 |
| 25 |
| MQ |
| MC |
| HQ |
| AC |
| ||
| x+2 |
解答: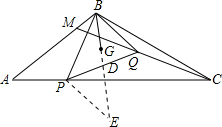 解:(1)延长BG,交边PQ于点D,由点G是△BPQ的重心,可知PD=DQ,
解:(1)延长BG,交边PQ于点D,由点G是△BPQ的重心,可知PD=DQ,
延长BD至点E,使DE=BD,连接PE,
∵PD=DQ,DE=BD,∠PDE=∠QDB,
∴△PDE≌△QDB,
∴PE=BQ,∠PED=∠QBD,
∵∠QBG=∠BAC,
∴∠PED=∠BAC,
∵∠PBG=∠BCA,
∴△BPE∽△CBA,
∴
=
=
,
∴
=
;
(2)延长AB至点F,使BF=AB,连接QF,过点Q作QH∥AC,交边AB于点H,
∵
=
,
=
,
∴
=
,
∵∠PBQ=∠BAC+∠BCA,∠CBF=∠BAC+∠BCA,
∴∠PBQ=∠CBF,
∴∠PBC=∠QBF,
∴△PBC∽△QBF,
∴∠BCP=∠BFQ,
=
=
,
∵HQ∥AC,
∴∠BHQ=∠BAC,
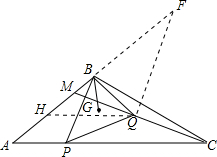 ∴△FQH∽△CBA,
∴△FQH∽△CBA,
∴
=
=
,
∴
•
=(
)2,即
=
,
∴HQ=
PC=
x,
∵HQ∥AC,
∴
=
,即y=
,
∴y关于x的函数关系式为:y=
.
 解:(1)延长BG,交边PQ于点D,由点G是△BPQ的重心,可知PD=DQ,
解:(1)延长BG,交边PQ于点D,由点G是△BPQ的重心,可知PD=DQ,延长BD至点E,使DE=BD,连接PE,
∵PD=DQ,DE=BD,∠PDE=∠QDB,
∴△PDE≌△QDB,
∴PE=BQ,∠PED=∠QBD,
∵∠QBG=∠BAC,
∴∠PED=∠BAC,
∵∠PBG=∠BCA,
∴△BPE∽△CBA,
∴
| BP |
| PE |
| BC |
| AB |
| 5 |
| 4 |
∴
| BP |
| BQ |
| 5 |
| 4 |
(2)延长AB至点F,使BF=AB,连接QF,过点Q作QH∥AC,交边AB于点H,
∵
| BP |
| BQ |
| 5 |
| 4 |
| BC |
| BF |
| 5 |
| 4 |
∴
| BP |
| BQ |
| BC |
| BF |
∵∠PBQ=∠BAC+∠BCA,∠CBF=∠BAC+∠BCA,
∴∠PBQ=∠CBF,
∴∠PBC=∠QBF,
∴△PBC∽△QBF,
∴∠BCP=∠BFQ,
| PC |
| QF |
| BP |
| BQ |
| 5 |
| 4 |
∵HQ∥AC,
∴∠BHQ=∠BAC,
 ∴△FQH∽△CBA,
∴△FQH∽△CBA,∴
| QF |
| HQ |
| BC |
| AB |
| 5 |
| 4 |
∴
| PC |
| QF |
| QF |
| HQ |
| 5 |
| 4 |
| PC |
| HQ |
| 25 |
| 16 |
∴HQ=
| 16 |
| 25 |
| 16 |
| 25 |
∵HQ∥AC,
∴
| MQ |
| MC |
| HQ |
| AC |
| ||
| x+2 |
∴y关于x的函数关系式为:y=
| 16x |
| 25x+50 |
点评:此题考查了相似形的综合,用到的知识点是相似三角形的判定与性质、平行线分线段成比例定理、三角形的重心,关键是做出辅助线,构造相似三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
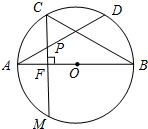 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是
 如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.
如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,船P在船B的北偏西30°方向上,BP的距离为30海里.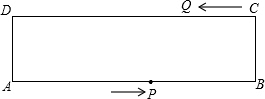 如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过