题目内容
6. 若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$.
若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$.
分析 根据正数的绝对值是它本身,负数的绝对值是它的相反数,可化简绝对值,根据二次根式的性质,可化简二次根式,根据整式的加减,可得答案.
解答 解:如图:
|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$=-a+0-(c-a)-2(-c)
=-a-c+a+2c
=c.
点评 本题考查了实数与数轴,利用绝对值的性质、二次根式的性质化简是解题关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
17.下列计算正确的是( )
| A. | 3a+2b=5ab | B. | x+x=x2 | C. | 5y2-2y2=3 | D. | -x3+3x3=2x3 |
11.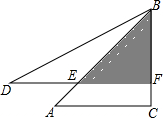 将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )
将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )
 将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )
将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
18.下列方程中,x-1=0的解是( )
| A. | x=0 | B. | x=1 | C. | x=-1 | D. | x=2 |
15.已知二次函数y=a(x-1)2+c(a>0),当自变量x分别取-$\sqrt{3}$、0、3时,对应的函数值分别为:y1,y2,y3,则y1,y2,y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y3<y1<y2 | D. | y2<y3<y1 |
16.下列关于有理数加减法表示正确的是( )
| A. | a>0 b<0,并且|a|>|b|,则a+b=|a|+|b| | B. | a<0 b>0,并且|a|>|b|,则a+b=|a|-|b| | ||
| C. | a<0 b>0,并且|a|<|b|,则a-b=|b|+|a| | D. | a<0 b<0,并且|a|>|b|,则a-b=|b|-|a| |
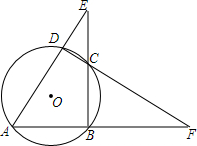 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.