题目内容
16.(1)计算:3(4+1)(42+1)(44+1)+1(2)分解因式:ab-2a-3b+6.
分析 (1)原式变形后,利用平方差公式计算即可得到结果;
(2)原式结合后,提取公因式即可得到结果.
解答 解:(1)原式=(4-1)(4+1)(42+1)(44+1)+1
=(42-1)(42+1)(44+1)+1
=(44-1)(44+1)+1
=48-1+1
=48
=216;
(2)原式=ab-3b-2(a-3)
=b(a-3)-2(a-3)
=(a-3)(b-2).
点评 此题考查了平方差公式,以及因式分解-分组分解法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.圆、平行四边形、等腰三角形、菱形,矩形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
11.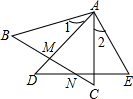 如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )
如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )
 如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )
如图,△ABC和△ADE中∠1=∠2,BC交AD于M,AC交DE于N,则图中全等三角形的对数有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
1.若(x-1)0=1,求x的取值范围( )
| A. | x≤1 | B. | x≥1 | C. | x≠1 | D. | x=1 |
5.下列四个图案中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

 若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$.
若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$.