题目内容
11.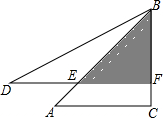 将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )
将一副三角板(一个等腰直角三角形和一个锐角为60°的直角三角形)如图所示叠放在一起,若DB=20,则阴影部分的面积为( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
分析 由于DF∥AC,那么△BEF也是等腰直角三角形,欲求其面积,必须先求出直角边BF的长;Rt△DBF中,已知斜边BD及∠D的度数,易求得BF的长,进而可根据三角形面积的计算方法求出阴影部分的面积.
解答 解:∵∠D=30°,∠BFE=90°,BD=20,
∴BF=10.
由题意可知DF∥AC,
∴∠BFE=∠BCA=45°,
∴BF=EF=10.
故S△BEF=$\frac{1}{2}$×10×10=50.
故选A.
点评 本题考查了相似三角形的判定和性质以及解直角三角形,发现△ACF是等腰直角三角形,并能根据直角三角形的性质求出直角边AC的长,是解答此题的关键.

练习册系列答案
相关题目
1.若(x-1)0=1,求x的取值范围( )
| A. | x≤1 | B. | x≥1 | C. | x≠1 | D. | x=1 |
20.下列各式运算正确的是( )
| A. | (a-2)(2+a)=22-a2 | B. | (x+2)(2x-2)=2x2-4 | C. | (-a-b)(a+b)=a2-b2 | D. | (ab-3)(ab+3)=a2b2-9 |
1. 如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )
如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )
 如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )
如图,点A,B,C在⊙O上,⊙O的半径为9,弧AB的长为2π,则∠ACB的大小是( )| A. | 20° | B. | 45° | C. | 60° | D. | 40° |
 若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$.
若实数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简|a|+|a+b|-$\sqrt{{{(c-a)}^2}}$一2$\sqrt{c^2}$.