题目内容
7.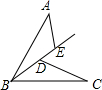 如图,点D在射线BE上,BA=BC,∠AEB=∠BDC,∠A=∠CBD.
如图,点D在射线BE上,BA=BC,∠AEB=∠BDC,∠A=∠CBD.(1)求证:△ABE≌△BCD;
(2)若AE=3,CD=5,求DE的长.
分析 (1)由已知条件,根据AAS定理可直接证得△ABE≌△BCD;
(2)由△ABE≌△BCD,可得到AE=BD=3,CD=BE=5,则DE=BE-BD=2.
解答 (1)证明:在△ABE和△BCD中,
$\left\{\begin{array}{l}{BA=BC}\\{∠AEB=∠BDC}\\{∠A=∠C}\end{array}\right.$
∴△ABE≌△BCD;
(2)解:由(1)知:∴△ABE≌△BCD,
∴AE=BD=3,CD=BE=5,
∴DE=BE-BD=2.
点评 本题主要考查了全等三角形的判定与性质,线段的和差计算,熟练掌握三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
18.下列图形是正方形展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
2.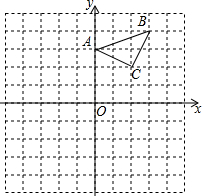 如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )
如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )
 如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )
如图,已知△ABC在平面直角坐标系中,点A的坐标为(0,3),若以点B为位似中心,在平面直角坐标系内画出△A′BC′,使得△A′BC′与△ABC位似,且相似比为2:1,则点C′的坐标为( )| A. | (0,0) | B. | (0,1) | C. | (1,-1) | D. | (1,0) |
16.下列几何体中,左视图与主视图不相同的只可能是( )
| A. |  | B. |  | C. |  | D. |  |
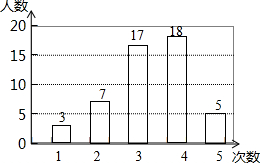 某校为了解全校1500名学生参加社会实践活动的情况,随机调查了50名学生每人参加社会实践活动的次数,并根据数据绘成条形统计图如下:
某校为了解全校1500名学生参加社会实践活动的情况,随机调查了50名学生每人参加社会实践活动的次数,并根据数据绘成条形统计图如下:
 如图,∠A=90°,∠ABC的角平分线交AC于E,AE=3,则E到BC的距离为3.
如图,∠A=90°,∠ABC的角平分线交AC于E,AE=3,则E到BC的距离为3.