题目内容
15.已知关于x的二次函数y=-x2-2x-$\frac{m}{2}$与x轴有两个交点,m为正整数.(1)当-x2-2x-$\frac{m}{2}$=0时,求m的值;
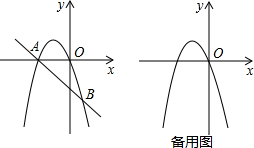
(2)如图,当该二次函数的图象经过原点时,与直线y=-x-2的图象交于A,B两点,求A,B两点的坐标;
(3)将(2)中的二次函数图象x轴上方的部分沿x轴翻折到x轴下方,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M”形状的新图象.现有直线y=a(a≠0)与该新图象恰好有两个公共点,直接写出a的取值范围.
分析 (1)根据根的判别式,可得不等式,根据解不等式,可得答案;
(2)根据解方程组,可得交点坐标;
(3)根据翻折的性质,可得新函数翻折部分的顶点的纵坐标为-1,根据平行于x轴的直线与新函数翻折部分没有交点,可得答案.
解答 解:(1)由-x2-2x-$\frac{m}{2}$=0有两个不相等实数根,
∴△=b2-4ac=(-2)2-4×(-1)×(-$\frac{m}{2}$)>0,
解得m<2.由m是正整数,
m=1;
(2)联立抛物线与直线y=-x-2,得
$\left\{\begin{array}{l}{y=-{x}^{2}-2x}\\{y=-x-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=-3}\end{array}\right.$,$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$,
A的坐标(-2,0),点B的坐标(1,-3);
(3)如图 ,
,
由翻折的性质,得
新函数翻折部分的顶点的纵坐标为-1,
当a<-1时,直线y=a(a≠0)与该新图象恰好有两个公共点.
直线y=a(a≠0)与该新图象恰好有两个公共点,a的取值范围是a<-1.
点评 本题考查了二次函数综合题,利用根的判别式得出不等式是解题关键;利用解方程组是求交点坐标的关键;利用平行于x轴的直线与新函数翻折部分没有交点是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.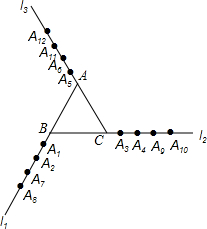 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )| A. | 在直线l1上 | B. | 在直线l2上 | ||
| C. | 在直线l3上 | D. | 不能确定在哪条直线上 |
10.下列图形中,∠1与∠2互为补角的是( )
| A. |  | B. |  | C. |  | D. |  |
20.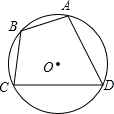 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ADC=60°,则劣弧AC的长为( )| A. | 2π | B. | 4π | C. | 5π | D. | 6π |
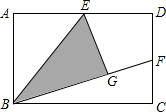 (1)如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)如图,矩形ABCD中,E是AD中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.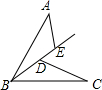 如图,点D在射线BE上,BA=BC,∠AEB=∠BDC,∠A=∠CBD.
如图,点D在射线BE上,BA=BC,∠AEB=∠BDC,∠A=∠CBD. 已知等腰△DEF中,DE=DF,求作△DEF的外接圆.(尺规作图,保留作图痕迹)
已知等腰△DEF中,DE=DF,求作△DEF的外接圆.(尺规作图,保留作图痕迹)