题目内容
2.如图,在平面直角坐标系中,⊙O交x轴于A、B两点,点P为圆上一动点PQ⊥x轴于点Q,点P运动到某一时刻:PQ=$\sqrt{3}$,AQ=3.(1)求⊙O的半径;
(2)当点C(m,n)在第三象限的圆弧上运动,CD⊥x轴于D,在x轴上取一点I(点I在点D的左侧),使ID=CD,过点I作x 轴的垂线,并在垂线上取一点T(点T在x轴上方),将TC绕点T逆时针旋转90°得到线段TM,MN⊥x轴于点N,设IT=p,MN=q,判断关于x的方程:nx2+qx-p=0根的情况;
(3)在(2)的条件下,作直线MI,判断当点P运动过程中,直线MI与⊙O的位置关系,并判断m的取值情况.
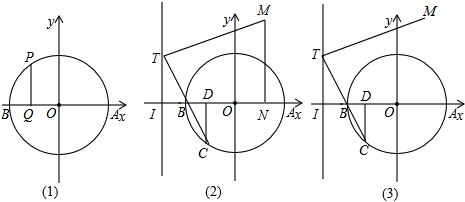
分析 (1)根据sin∠PAQ=$\frac{PQ}{PA}$=$\frac{PB}{AB}$即可解决问题.
(2)如图2中,作TG⊥MN于G,CK⊥TI于K,先证明△KTC≌△GTM,再证明四边形TING是矩形,得q=p-n,再利用判别式即可解决问题.
(3)如图2中,当OC∥MI时,作OH⊥MI,求出相切时m的值即可解决问题.
解答 解:(1)如图1中, 连接PA、PB.
连接PA、PB.
∵AB是直径,
∴∠APB=90°,
∵∠PQA=90°,PQ=$\sqrt{3}$,AQ=3,
∴PA=$\sqrt{P{Q}^{2}+A{Q}^{2}}$=2$\sqrt{3}$,sin∠PAQ=$\frac{PQ}{PA}$=$\frac{1}{2}$,
∴∠PAB=30°,
∴PB=PA•tan30°=2$\sqrt{3}$•$\frac{\sqrt{3}}{3}$=2,
∴AB=2PB=4,
∴⊙O 的半径为2.
(2)如图2中,作TG⊥MN于G,CK⊥TI于K.
∵∠CKI=∠KID=∠CDI=90°,
∴四边形CDIK是矩形,
∵ID=CD,
∴四边形CDIK是正方形,
∴CD=KC,
∵∠KTG=∠CTM=90°,
∴∠KTC=∠GTM,
在△KTC和△GTM中,
$\left\{\begin{array}{l}{∠TKC=∠TGM}\\{∠KTC=∠GTM}\\{TC=TM}\end{array}\right.$,
∴△KTC≌△GTM,
∴KC=MG=CD=-n,
∵∠TIN=∠TGN=∠GNI=90°,
∴四边形TING是矩形,
∴TI=GN=p,
∴MN=MG+GN,
∴q=P+(-n)=P-n,
∵关于x的方程:nx2+qx-p=0,△=q2+4np=(p-n)2+4np=(p+n)2>0,
∴方程有两个不相等的实数根.
(3)如图2中,当OC∥MI时,作OH⊥MI,
∵四边形HICO是正方形,
∴∠KIC=45°,
∵△TCM是等腰直角三角形,
∴∠TMC=45°,
∴∠KIC=∠TMC,
∴T、I、C、M四点共圆,
∴∠CIM=∠CTM=90°,
∵OC∥IM,
∴∠ICO=90°,
∵∠HIC=∠ICO=∠IHO=90°,
∴四边形IHOC是矩形,
∵∠CIO=∠CIO=45°,
∴CI=CO,
∴四边形OCIH是正方形,
∴OH=OC,
∴直线MI是⊙O的切线,
∵CO=CI=2,
∴IC=2$\sqrt{2}$,CD=$\sqrt{2}$,
∴点C坐标(-$\sqrt{2}$,-$\sqrt{2}$)时直线MI与⊙O相切,
∴当m=-$\sqrt{2}$时,直线IM与⊙O相切,当-2<m<-$\sqrt{2}$或-$\sqrt{2}$<m<0时,直线MI与⊙O相切.
点评 本题考查圆的有关知识、全等三角形的判定和性质、切线的判定和性质、等腰直角三角形的性质等知识,解决问题的关键是添加辅助线构造全等三角形,属于中考压轴题.

| A. | 有一腰和一角对应相等 | B. | 有两角一边对应相等 | ||
| C. | 有顶角和一个底角对应相等 | D. | 有两角对应相等 |
