题目内容
10．菱形的两邻角的度数之比为1：3，高为7$\sqrt{2}$，则其面积S=98$\sqrt{2}$．分析 根据菱形的两邻角是同旁内角互补可求菱形的每个内角的度数，因为菱形的高与菱形的两边所构成的直角三角形为等腰直角三角形，则可求出菱形的边长，进而可求出其面积．
解答 解：菱形两邻角是同旁内角互补，即菱形两邻角的和是180°．
因为菱形两邻角的度数之比为1：3，则可以求出这两个角是45°和135°．
菱形的高与菱形的两边所构成的直角三角形是等腰直角三角形，那么它的斜边即菱形的边长=$\sqrt{98+98}$=14，
则面积=边长×高=14×7$\sqrt{2}$=98$\sqrt{2}$．
故答案为98$\sqrt{2}$．
点评 本题考查了菱形的性质、等腰直角三角形的判定与性质以及勾股定理的运用；熟练掌握菱形的性质，证明三角形是等腰直角三角形是解决问题的关键．
练习册系列答案
相关题目
如图，在△ABC中，∠A=40°，∠B=72°，CD是AB边上的高，CE是∠ACB的平分线，DF⊥CE于F，求∠CDF的度数．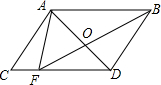
如图，平行四边形ABDC的面积为112平方厘米，又知AB=4CF，求三角形AOF的面积．
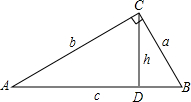小叶从计算中得到这样的结论：如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．设BC=a，AC=b，AB=c，CD=h，则有等式$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$成立．请你判断小叶的结论是否正确？若正确，请给予证明；若不正确，请说明理由．
19．某中学举行了一次演讲比赛，分段统计参赛同学的成绩，结果如下表（分数均为整数，满分为100分）：
根据表中提供的信息，回答下列问题：
①参加这次演讲比赛的同学共20人；
②成绩在91～100分的为优胜者，优胜率为20%．
| 分数段 | 61～70 | 71～80 | 81～90 | 91～100 |
| 人数（人） | 2 | 8 | 6 | 4 |
①参加这次演讲比赛的同学共20人；
②成绩在91～100分的为优胜者，优胜率为20%．
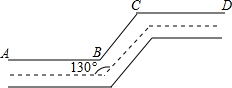如图，一条公路两次转完后又回到原来的方向（即AB∥CD），如果第一次转弯时的∠B=130°，那么第二次转弯时的∠C=130度．