题目内容
13.在△ABC中,AB=AC=5,BC=8,AD⊥BC于点D,求△ABC面积.分析 利用等腰三角形的性质求得BD=$\frac{1}{2}$BC=4.然后在直角△ABD中,利用勾股定理来求AD的长度,即可得出答案.
解答  解:如图,∵△ABC中,AB=AC=5,BC=8,AD⊥BC于点D,
解:如图,∵△ABC中,AB=AC=5,BC=8,AD⊥BC于点D,
∴BD=$\frac{1}{2}$BC=4,
∴在直角△ABD中,由勾股定理,得
AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3,
∴△ABC的面积为:$\frac{1}{2}$×BC×AD=$\frac{1}{2}×8×3$=12.
点评 此题主要考查了勾股定理,等腰三角形的性质的理解及运用.利用等腰三角形“三线合一”的性质求得AD的长度是解题的关键.

练习册系列答案
相关题目
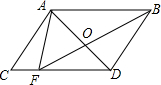 如图,平行四边形ABDC的面积为112平方厘米,又知AB=4CF,求三角形AOF的面积.
如图,平行四边形ABDC的面积为112平方厘米,又知AB=4CF,求三角形AOF的面积.