题目内容

1．已知a+b=-5，ab=-6，则a2+ab+b2=31．

分析 把a+b=-5两边平方，利用完全平方公式化简，再将ab=-6代入求出a2+b2的值，即可确定出所求式子的值．

解答 解：把a+b=-5两边平方得：（a+b）2=a2+2ab+b2=25，
把ab=-6代入得：a2+b2=37，
则原式=37-6=31，
故答案为：31

点评 此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．

练习册系列答案
相关题目
11．在?ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF=BE，连接AF，BF．
（1）求证：四边形DEBF是矩形；
（2）若AF平分∠DAB，AE=3，BF=4，求?ABCD的面积．
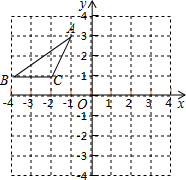12．如图，在平面直角坐标系中，点A、B、C的坐标分别为（-1，3）、（-4，1）（-2，1），先将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是（1，2），再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2，点A1的对应点为点A2．
（1）画出△A1B1C1；
（2）画出△A2B2C2；
（3）求出在旋转过程中，点A1到达A2的路径长．
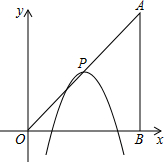9．如图，在平面直角坐标系中，点A，B的坐标分别为（6，6），（6，0），抛物线y=-（x-m）2+n的顶点P在折线OA-AB上运动．
（1）当点P在线段OA上运动时，抛物线y=-（x-m）2+n与y轴交点坐标为（0，c）．
①用含m的代数式表示n，
②求c的取值范围．
（2）当抛物线y=-（x-m）2+n经过点B时，求抛物线所对应的函数表达式；
（3）当抛物线与△ABO的边有三个公共点时，直接写出点P的坐标．
16．计算x5÷x3结果是x2．
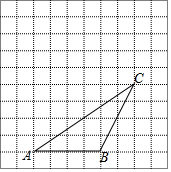6．如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移2格．
（1）请在图中画出平移后的△A′B′C′．
（2）作出△ABC的中线BD；
（3）求出△A′B′C′的面积．
13．下列计算：
①x（2x2-x+1）=2x3-x2+1；②（a-b）2=a2-b2；
③（x-4）2=x2-4x+16；      ④（5a-1）（-5a-1）=25a2-1；
⑤（-a-b）2=a2+2ab+b2．
其中正确的有（　　）
A．1个B．2个C．3个D．4个
10．已知xa=3，xb=5，则x2a-b（　　）
A．$\frac{6}{5}$B．$\frac{5}{6}$C．$\frac{9}{5}$D．$\frac{5}{9}$
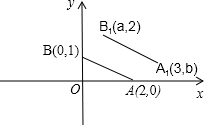11．如图，A，B两点的坐标分别为（2，0）（0，1），若将线段AB平移至A1B1，则a+b的值为（　　）
A．5B．4C．3D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网