题目内容
11. 在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求?ABCD的面积.
分析 (1)根据平行四边形性质得出DF∥BE,得出平行四边形BFDE,根据矩形的判定得出即可;
(2)根据矩形的性质求出BF=DE=4,根据勾股定理求出AD,求出AD=DF,得出AB,即可得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴DF∥BE,
又∵DF=BE,
∴四边形DEBF是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四形DEBF是矩形;
(2)解:∵四边形DEBF是矩形,
∴DF∥AB,DE=BF=4,DF=BE,
∴∠DAF=∠FAB,
又∵AF平分∠DAB,
∴∠DAF=∠FAB,
∴∠DFA=∠DAF,
∴DA=DF,
又∵DE⊥AB,
∴∠DEA=90°,
在Rt△ADE中
AD=$\sqrt{A{E}^{2}+D{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BE=5,
∴AB=AE+BE=3+5=8,
∴?ABCD的面积=AB•BF=8×4=32.
点评 本题考查了平行线的性质,平行四边形的性质和判定,勾股定理,矩形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.M国股民吉姆上周末买进某公司月股票1000股,每股27 元,下表为本周内每日该股的涨跌情况 (星期六、日股市休市) (单位:元)
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价多少元?最低价是多少元?
(3)已知吉姆买进股票时付了1.5%的手续费,卖出时还需付成交额1.5%的手续费和1%的交易税,如果吉姆在星期五收盘前将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +6 | +6.5 | -1 | -2.5 | -6 |
(2)本周内每股最高价多少元?最低价是多少元?
(3)已知吉姆买进股票时付了1.5%的手续费,卖出时还需付成交额1.5%的手续费和1%的交易税,如果吉姆在星期五收盘前将全部股票卖出,他的收益情况如何?
6.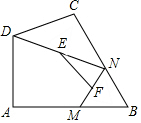 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )| A. | $\sqrt{7}$ | B. | 4 | C. | 3 | D. | 2 |
16.关于x,y的二元一次方程组$\left\{\begin{array}{l}x+y=9k\\ x-y=5k\end{array}\right.$的解也是二元一次方程2x+3y=6的解,则k的值为( )
| A. | $\frac{3}{10}$ | B. | $\frac{10}{3}$ | C. | $-\frac{3}{10}$ | D. | $-\frac{10}{3}$ |
3.要反映宝应县一周内气温的变化情况宜采用( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
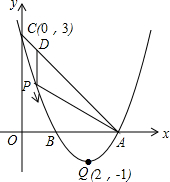 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.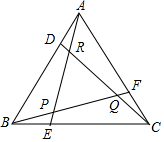 如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若$\frac{AD}{AB}$=$\frac{BE}{BC}$=$\frac{CF}{CA}$=k(0<k<$\frac{1}{2}$).
如图,△ABC是边长为m的正三角形,D,E,F分别在边AB,BC,CA上,AE,BF交于点P,BF,CD交于点Q,CD,AE交于点R,若$\frac{AD}{AB}$=$\frac{BE}{BC}$=$\frac{CF}{CA}$=k(0<k<$\frac{1}{2}$).