题目内容
5.先化简.再求值:$\frac{{y}^{2}}{xy+2{y}^{2}}$-$\frac{1}{y-1}$÷$\frac{x+2y}{{y}^{2}-2y+1}$,其中3x+6y-1=0.分析 先将原式化简,然后将3x+6y=1代入即可求出答案.
解答 解:由于3x+6y=1,
∴x+2y=$\frac{1}{3}$
∴原式=$\frac{{y}^{2}}{y(x+2y)}$-$\frac{1}{y-1}$×$\frac{(y-1)^{2}}{x+2y}$
=$\frac{y}{x+2y}$-$\frac{y-1}{x+2y}$
=$\frac{1}{x+2y}$
=3
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
16.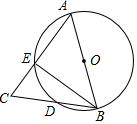 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )| A. | 22.5° | B. | 23° | C. | 25° | D. | 30° |
13.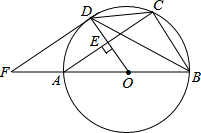 如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( )
如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( )
 如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( )
如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( )| A. | ∠CDB=∠BFD | B. | △BAC∽△OFD | C. | DF∥AC | D. | OD=BC |
17. 如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
 如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )| A. | 俯视图与主视图相同 | B. | 左视图与主视图相同 | ||
| C. | 左视图与俯视图相同 | D. | 三个视图都相同 |
14. 如图是由四个相同的小立方体搭成的几何体,它的主视图是( )
如图是由四个相同的小立方体搭成的几何体,它的主视图是( )
 如图是由四个相同的小立方体搭成的几何体,它的主视图是( )
如图是由四个相同的小立方体搭成的几何体,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
15.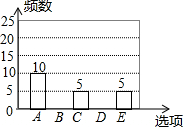 随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):
随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
 随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):
随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):| 选项 | 频数 | 频率 |
| A | 10 | m |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | p | 0.4 |
| E | 5 | 0.1 |
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
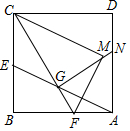 在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.
在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.