题目内容
1．解不等式组，并把解集表示在数轴上，并写出其整数解．$\left\{\begin{array}{l}{x-3≤0}\\{\frac{x-1}{2}+\frac{2x-1}{3}＞1}\end{array}\right.$．
分析 分别求出每一个不等式的解集，根据口诀：大小小大中间找确定不等式组的解集，再根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则在数轴上将解集表示出来，结合数轴可知其整数解．
解答 解：解不等式x-3≤0，得：x≤3，
解不等式$\frac{x-1}{2}$+$\frac{2x-1}{3}$＞1，得：x＞$\frac{11}{7}$，
∴不等式组的解集为：$\frac{11}{7}$＜x≤3，
将不等式解集表示在数轴上如图：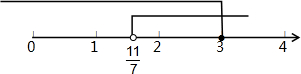
则该不等式组的整数解为2，3．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
图中所示为一组护网的示意图，它可以看成由两组平行线组成，你能通过检验一些角得大小来判断其中的线段是否平行吗？说出你的理由．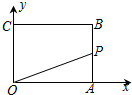
如图，在矩形OABC中，已知A（6，0），C（0，4），动点P从点A出发，沿A-B-C-O的路线匀速运动，设动点P的运动时间为t，△OAP的面积为S，则下列能大致反映S与t之间关系的图象是（ ）
如图，反比例函数y=$\frac{k}{x}$图象上有一点P，PA⊥x轴于点A，点B在y轴的负半轴上，若△PAB的面积为4，则k=-8．
如图AB是半圆的直径，C是半圆上一点，∠CAB=30°，AB=4则圆中阴影部分的面积为（$\frac{4π}{3}$-$\sqrt{3}$）cm2．
平面直角坐标系中，线段AB端点的坐标分别为A（-2，0），B（0，2），平移后，点A的对应点A′的坐标为A′（0，-1），则点B的对应点B′的坐标为（2，1）．线段AB平移的距离为$\sqrt{5}$．