题目内容
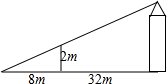 如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为
如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为考点:相似三角形的应用
专题:
分析:由已知可得BC∥DE,因此△ABC∽△ADE,利用相似三角形的性质可求得水塔的高度.
解答: 解:∵BC⊥AD,ED⊥AD,
解:∵BC⊥AD,ED⊥AD,
∴BC∥DE,
∴△ABC∽△ADE,
∴
=
,即
=
,
∴DE=10,即水塔的高度是10米.
故答案为:10.
 解:∵BC⊥AD,ED⊥AD,
解:∵BC⊥AD,ED⊥AD,∴BC∥DE,
∴△ABC∽△ADE,
∴
| BC |
| DE |
| AB |
| AD |
| 2 |
| DE |
| 8 |
| 8+32 |
∴DE=10,即水塔的高度是10米.
故答案为:10.
点评:本题考查了考查了相似三角形的判定和性质,解题的关键是能利用比例式求解线段长.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/小时)情况,则下列关于车速描述错误的是( )
如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/小时)情况,则下列关于车速描述错误的是( )| A、平均数是23 |
| B、中位数是25 |
| C、众数是30 |
| D、方差是129 |
下列运算正确的是( )
| A、a2•a3=a6 |
| B、(a2)3=a5 |
| C、2a2+3a2=5a6 |
| D、(a+2b)(a-2b)=a2-4b2 |
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电量15万度.如果设上半年每月平均用电x度,则所列方程正确的是( )
| A、6x+6(x-2000)=150000 |
| B、6x+6(x+2000)=150000 |
| C、6x+6(x-2000)=15 |
| D、6x+6(x+2000)=15 |
 如图,已知∠C=∠D,∠CAB=∠DBA,AD交BC于点O,请写出图中一组相等的线段
如图,已知∠C=∠D,∠CAB=∠DBA,AD交BC于点O,请写出图中一组相等的线段 如图,边长为2的正方形ABCD中,BD为对角线.AE∥BD,且DE=DB,DE与AB交于点F,则AE=
如图,边长为2的正方形ABCD中,BD为对角线.AE∥BD,且DE=DB,DE与AB交于点F,则AE= 如图,抛物线y=
如图,抛物线y=