题目内容
下列运算正确的是( )
| A、a2•a3=a6 |
| B、(a2)3=a5 |
| C、2a2+3a2=5a6 |
| D、(a+2b)(a-2b)=a2-4b2 |
考点:平方差公式,合并同类项,同底数幂的乘法,幂的乘方与积的乘方
专题:
分析:根据同底数幂的乘法,可判断A,根据幂的乘方,可判断B,根据合并同类项,可判断C,根据平方差公式,可判断D.
解答:解:A、底数不变指数相加,故A错误;
B、底数不变指数相乘,故B错误;
C、系数相加字母部分不变,故C错误;
D、两数和乘以这两个数的差等于这两个数的平方差,故D正确;
故选:D.
B、底数不变指数相乘,故B错误;
C、系数相加字母部分不变,故C错误;
D、两数和乘以这两个数的差等于这两个数的平方差,故D正确;
故选:D.
点评:本题考查了平方差,利用了平方差公式,同底数幂的乘法,幂的乘方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在一次捐款活动中,某校七年级(1)班6名团员的捐款金额(单位:元)如下:10,15,30,50,30,20.这级数据的众数是( )
| A、10 | B、15 | C、20 | D、30 |
不等式组
的解集是( )
|
A、-1≤x<
| ||
B、-
| ||
C、-
| ||
| D、1≤x<2 |
某商场四月份的利润是28万元,预计六月份的利润将达到40万元.设利润每月平均增长率为x,则根据题意所列方程正确的是( )
| A、28(1+x)2=40 |
| B、28(1+x)2=40-28 |
| C、28(1+2x)=40 |
| D、28(1+x2)=40 |
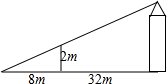 如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为
如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为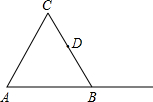 如图,△ABC是等边三角形,D是BC的中点.
如图,△ABC是等边三角形,D是BC的中点. 如图,?ABCD中,点E在边AB上,点F在AB的延长线上,且AE=BF.求证:∠ADE=∠BCF.
如图,?ABCD中,点E在边AB上,点F在AB的延长线上,且AE=BF.求证:∠ADE=∠BCF.