题目内容
 如图,边长为2的正方形ABCD中,BD为对角线.AE∥BD,且DE=DB,DE与AB交于点F,则AE=
如图,边长为2的正方形ABCD中,BD为对角线.AE∥BD,且DE=DB,DE与AB交于点F,则AE=考点:正方形的性质,含30度角的直角三角形,解直角三角形
专题:
分析:根据正方形的性质求出∠DAE=135°,DE=2
,借助余弦定理求出AE的长度.
| 2 |
解答:解:∵四边形ABCD是正方形,
∴∠C=∠DAB=90°,∠ABD=45°;
又∵AE∥BD,
∴∠BAE=∠ABD=45°,
∴∠DAE=135°;
由勾股定理得:BD=
=2
;
故DE=BD=2
;
设AE=x,由余弦定理得:
(2
)2=22+x2-2×2xcos135°,
整理得:x2+2
x-4=0,
解得x=
-
或-
-
(不合题意,舍去).
故答案是:
-
.
∴∠C=∠DAB=90°,∠ABD=45°;
又∵AE∥BD,
∴∠BAE=∠ABD=45°,
∴∠DAE=135°;
由勾股定理得:BD=
| 22+22 |
| 2 |
故DE=BD=2
| 2 |
设AE=x,由余弦定理得:
(2
| 2 |
整理得:x2+2
| 2 |
解得x=
| 6 |
| 2 |
| 6 |
| 2 |
故答案是:
| 6 |
| 2 |
点评:考查了正方形的性质.解题的关键是借助余弦定理求出AE的长度.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 如图,计算所给三视图表示的几何体的体积是
如图,计算所给三视图表示的几何体的体积是 数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.
数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.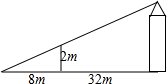 如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为
如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为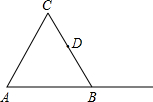 如图,△ABC是等边三角形,D是BC的中点.
如图,△ABC是等边三角形,D是BC的中点.