题目内容
6．在?ABCD中，延长AD到F，使DF=AD，连接BF交CD于E，求证：点E平分CD、BF．分析 根据平行四边形的性质可得AD∥BC，AD=BC，进而可得∠CBE=∠F，DF=BC，再证明△BCE≌△FDE（AAS），可得BE=FE，DE=CE，进而可得结论．
解答 证明：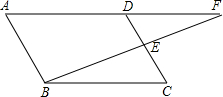
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠CBE=∠F，
∵DF=AD，
∴DF=BC，
在△BCE和△FDE中，$\left\{\begin{array}{l}{∠F=∠CBE}\\{∠DEF=∠CEB}\\{DF=BC}\end{array}\right.$，
∴△BCE≌△FDE（AAS），
∴BE=FE，DE=CE，
即点E是CD、BF的中点．
点评 此题主要考查了平行四边形的性质，关键是掌握平行四边形的对边相等且平行．
练习册系列答案
相关题目
16．下列计算正确的是（ ）
| A． | $-\frac{a}{-b}=\frac{a}{b}$ | B． | $\frac{{{x^2}-4}}{x-2}=x-2$ | C． | ${（{\frac{3y}{x}}）^2}=\frac{{6{y^2}}}{x^2}$ | D． | ${4^{-2}}=-\frac{1}{16}$ |
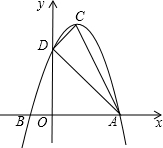如图，抛物线y=ax2+bx+c的顶点为C（1，4），交x轴于点A（3，0），B两点，交y轴于点D．
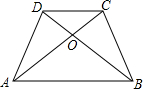如图，AD=BC，AC=BD，AC与BD相交于O点，则图中全等三角形共有3对．