题目内容
1.若a≠0,b≠0,则$\frac{a}{|a|}$+$\frac{b}{|b|}$的不同取值的个数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 分为a<0,b<0;a<0,b>0;a>0,b>0;a>0,b<0四种情况.
解答 解:①当a<0,b<0时,原式=$\frac{a}{-a}+\frac{b}{-b}=-1+(-1)=-2$;
②当a<0,b>0时,原式=$\frac{a}{-a}+\frac{b}{b}=-1+1=0$;
③当a>0,b>0时,原式=$\frac{a}{a}+\frac{b}{b}=1+1=2$;
④当a>0,b<0时,原式=$\frac{a}{a}+\frac{b}{-b}=1+(-1)=0$.
综上所述,共有3个不同的取值.
故选:A.
点评 本题主要考查的是绝对值的性质的应用,掌握绝对值的性质是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
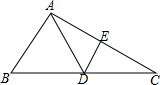 如图,在△ABC中,AC的垂直平分线交BC于点D,△ABD的周长为13,AE=3,则△ABC的周长为19.
如图,在△ABC中,AC的垂直平分线交BC于点D,△ABD的周长为13,AE=3,则△ABC的周长为19.