题目内容
6.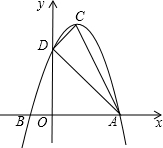 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D.(1)求点B、点D的坐标;
(2)判断△ACD的形状,并求出△ACD的面积;
(3)请探究抛物线上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?若存在,请求出此时点E的坐标;若不存在,请说明理由.
分析 (1)由顶点坐标和A点坐标,可求得抛物线的解析式,容易求出B、D的坐标;
(2)根据点的坐标,利用勾股定理可求得AD、AC、CD的长,可判断△ACD的形状;
(3)先利用待定系数法求出直线AD的解析式,过点C作CE∥AD,求出直线CE的解析式,联立直线CE与抛物线的解析式即可得出E点坐标,在直线CD上截取CD=DF,求出F点的坐标,过点F作FG∥AD,利用待定系数法求出直线FG的解析式,联立此直线与抛物线的解析式即可得出E点坐标.
解答 解:(1)∵抛物线的顶点坐标为(1,4),
∴可设抛物线解析式为y=a(x-1)2+4,
∵与x轴交于点A(3,0),
∴0=4a+4,解得a=-1,
∴抛物线解析式为y=-(x-1)2+4=-x2+2x+3,
令y=0,可得-x2+2x+3=0,解得x=-1或x=3,令x=0,可得y=3
∴B点坐标为(-1,0),D点坐标为(0,3);
(2)∵A(3,0),D(0,3),C(1,4),
∴AD=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,CD=$\sqrt{{(1-0)}^{2}+{(4-3)}^{2}}$=$\sqrt{2}$,AC=$\sqrt{(1-3)^{2}+(4-0)^{2}}$=2$\sqrt{5}$,
∴AD2+CD2=(3$\sqrt{2}$)2+($\sqrt{2}$)2=20=(2$\sqrt{5}$)2=AC2,
∴△ACD是以AC为斜边的直角三角形,
∴S△ACD=$\frac{1}{2}$AD•CD=$\frac{1}{2}$×3$\sqrt{2}$×$\sqrt{2}$=3;
(3)设直线AD的解析式为y=kx+b(k≠0),
∵A(3,0),D(0,3),
∴$\left\{\begin{array}{l}3k+b=0\\ b=3\end{array}\right.$,解得$\left\{\begin{array}{l}k=-1\\ b=3\end{array}\right.$,
∴直线AD的解析式为y=-x+3.
过点C作CE∥AD,则直线CE的解析式为y=-x+c(a≠0),
∵C(1,4),
∴-1+c=4,解得c=5,
∴直线CE的解析式为y=-x+5,
∴$\left\{\begin{array}{l}y=-x+5\\ y=-{x}^{2}+2x+3\end{array}\right.$,解得$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$,
∴E1(2,3);
设直线CD的解析式为y=mx+n(m≠0),
∵C(1,4),D(0,3),
∴$\left\{\begin{array}{l}4=m+n\\ 3=n\end{array}\right.$,解得$\left\{\begin{array}{l}m=1\\ n=3\end{array}\right.$,
∴直线CD的解析式为y=x+3.
∵CD=$\sqrt{(1-0)^{2}+(4-3)^{2}}$=$\sqrt{2}$,
∴DF=$\sqrt{2}$.
设F(x,x+3)且x<0,则DF=$\sqrt{{x}^{2}+{x}^{2}}$=$\sqrt{2}$,解得x=-1,
∴F(-1,2).
令直线FG的解析式为y=-x+d,则1+d=2,解得d=1,
∴直线FG的解析式为y=-x+1,
∴$\left\{\begin{array}{l}y=-x+1\\ y=-{x}^{2}+2x+3\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{3+\sqrt{17}}{2}\\ y=\frac{-1-\sqrt{17}}{2}\end{array}\right.$或$\left\{\begin{array}{l}x=\frac{3-\sqrt{17}}{2}\\ y=\frac{-1+\sqrt{17}}{2}\end{array}\right.$,
∴E2($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$),E3($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$).
综上所示,E1(2,3),E2($\frac{3+\sqrt{17}}{2}$,$\frac{-1-\sqrt{17}}{2}$),E3($\frac{3-\sqrt{17}}{2}$,$\frac{-1+\sqrt{17}}{2}$).
点评 本题考查的是圆的综合题,涉及到待定系数法及勾股定理的逆定理,根据抛物线的顶点坐标写出其顶点式求得抛物线的解析式是解题的关键.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案| A. | (a,$\sqrt{3}$a) | B. | (-a,-$\sqrt{3}$a) | C. | (-a,$\sqrt{3}$a) | D. | (-$\sqrt{3}$,a) |
| 捐款金额 | 5元 | 10元 | 15元 | 20元 | 50元 |
| 捐款人数 | 4人 | 12人 | 10 | 18人 | 6人 |
(1)七年级(1)班共有多少人?
(2)学生捐款金额的众数和中位数分别是多少元?
| A. | $\frac{25π}{2}$厘米 | B. | 15π厘米 | C. | $\frac{75π}{2}$厘米 | D. | 75π厘米 |
| 空气质量级别 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 10 | a | 4 | b | 3 | 2 |
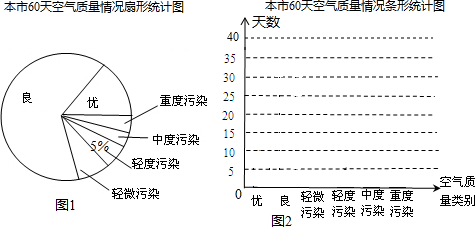
请你根据所给信息解答下列问题:
(1)求a,b的值;
(2)这次抽样中,“空气质量不低于良”的频率为$\frac{4}{5}$;
(3)画出本市60天空气质量情况条形统计图;
(4)根据这次抽样结果,请你估计2013年全年(共365天)空气质量为优良的天数是多少?
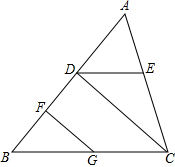 如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.
如图,已知∠ADE=∠B,∠EDC=∠FGB,GF⊥AB.试说明CD⊥AB.