题目内容
18．已知实数a，b，满足$\frac{\sqrt{3a-b}+|{a}^{2}-49|}{\sqrt{a+7}}$=0，c是$\sqrt{35}$的整数部分，求a+2b+3c的平方根．分析 根据分式和二次根式、绝对值有意义的条件求出a的值，再根据3a-b=0，求出b的值，根据c是$\sqrt{35}$的整数部分，求出c的值，把它们的值代入要求的式子，然后求求出平方根即可．
解答 解：∵实数a，b，满足$\frac{\sqrt{3a-b}+|{a}^{2}-49|}{\sqrt{a+7}}$=0，
∴a2-49=0，
∴a=±7，
∵a+7＞0，
∴a=7，
∵3a-b=0，
∴b=21，
∵c是$\sqrt{35}$的整数部分，
∴c=5，
∴a+2b+3c=7+2×21+3×5=64，
∴a+2b+3c的平方根为±8．
点评 此题考查了估算无理数的大小，用到的知识点是二次根式、平方根、分式的意义和绝对值等知识点，关键是根据已知条件求出a，b，c的值．
练习册系列答案
备战中考寒假系列答案
相关题目
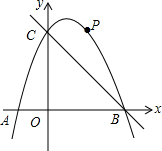如图，在平面直角坐标系中，二次函数y=-x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．
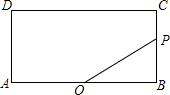如图，矩形ABCD中，AB=2，BC=1，O是AB的中点，动点P从B点开始沿着边BC，CD运动到点D结束．设BP=x，OP=y，则y关于x的函数图象大致为（ ）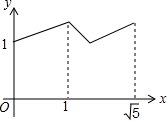
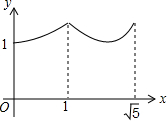
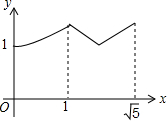
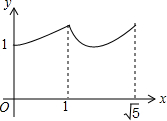
10．有一箱子装有3张分别标示4，5，6的号码牌，已知小明以每次取一张且取后不放回的方式，先后取出2张牌，组成一个二位数，则组成的二位数是6的倍数的概率是（ ）
| A． | $\frac{7}{12}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
解不等式$\frac{1}{2}（x+1）≤\frac{2}{3}x-1$，并把它的解集表示在数轴上，再写出它的最小整数解．