题目内容
6.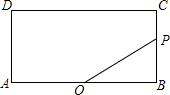 如图,矩形ABCD中,AB=2,BC=1,O是AB的中点,动点P从B点开始沿着边BC,CD运动到点D结束.设BP=x,OP=y,则y关于x的函数图象大致为( )
如图,矩形ABCD中,AB=2,BC=1,O是AB的中点,动点P从B点开始沿着边BC,CD运动到点D结束.设BP=x,OP=y,则y关于x的函数图象大致为( )| A. | 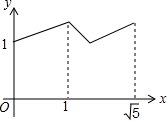 | B. | 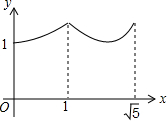 | ||
| C. | 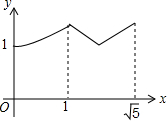 | D. | 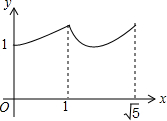 |
分析 根据题意和图象可以得到各段的函数解析式,从而可以得到函数所对应的图象,本题得以解决.
解答 解:当点P从点B运动到点C的过程中,
由题意可得,$y=\sqrt{{1}^{2}+{x}^{2}}$=$\sqrt{{x}^{2}+1}$(0≤x≤1),
当点P从C运动到线段CD的中点过程中,
由题意可得,y=$\sqrt{{1}^{2}+(1-\sqrt{{x}^{2}-1})^{2}}$=$\sqrt{{x}^{2}-2\sqrt{{x}^{2}-1}+1}$(1≤x≤$\sqrt{2}$),
当点P从CD的中点运动到点D的过程中,
由题意可得,y=$\sqrt{{1}^{2}+(\sqrt{{x}^{2}-1}-1)^{2}}$=$\sqrt{{x}^{2}-2\sqrt{{x}^{2}-1}+1}$($\sqrt{2}≤x≤\sqrt{5}$),
由上可得,在BC段的函数图象是曲线,y随x的增大而增大,y的最小值1;在点P从C运动到线段CD的中点过程中,图象是曲线,y随x的增大而减小;在点P从CD的中点运动到点D的过程中,图象是曲线,y随x的增大而增大.
故选D.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,可以列出各段的函数解析式,明确各段对应的函数图象.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图,在菱形ABCD中,∠B=60°,点E、F分别在边AB、AD上,且AE=DF.
如图,在菱形ABCD中,∠B=60°,点E、F分别在边AB、AD上,且AE=DF. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,求证:AE∥CF.
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,求证:AE∥CF.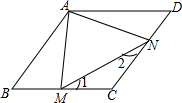 如图,在菱形ABCD中,M、N分别是边BC、CD上的点,且AM=AN=MN=AB,则∠C的度数为100°.
如图,在菱形ABCD中,M、N分别是边BC、CD上的点,且AM=AN=MN=AB,则∠C的度数为100°.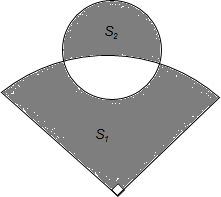 如图,在半径为5,圆心角为90°的扇形中,阴影部分的面积S1;在半径为2的圆中,阴影部分的面积为S2,则S1-S2=$\frac{9}{4}$π(结果保留π).
如图,在半径为5,圆心角为90°的扇形中,阴影部分的面积S1;在半径为2的圆中,阴影部分的面积为S2,则S1-S2=$\frac{9}{4}$π(结果保留π).