题目内容
 如图:直线y1=x+m分别与x轴、y轴交于A、B两点,与双曲线y2=
如图:直线y1=x+m分别与x轴、y轴交于A、B两点,与双曲线y2=| k |
| x |
(1)分别求出直线AB及双曲线的解析式.
(2)利用图象求出当y1>y2时x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把C(-1,2)分别代入y1=x+m,y2=
(x<0)根据待定系数法即可求得;
(2)联立方程,解方程即可求得D的坐标,根据图象即可求得y1>y2时x的取值范围.
| k |
| x |
(2)联立方程,解方程即可求得D的坐标,根据图象即可求得y1>y2时x的取值范围.
解答:解:(1)把C(-1,2)代入y1=x+m得:-1+m=2,
解得 m=3,
则y1=x+3,
把C(-1,2)代入y2=
(x<0)得:2=
,
解得:k=-2,
则y=-
;
(2)
,
解得:
或
,
则D点坐标为(-2,1),
由图可知:当-2<x<-1时,y1>y2.
解得 m=3,
则y1=x+3,
把C(-1,2)代入y2=
| k |
| x |
| k |
| -1 |
解得:k=-2,
则y=-
| 2 |
| x |
(2)
|
解得:
|
|
则D点坐标为(-2,1),
由图可知:当-2<x<-1时,y1>y2.
点评:本题考查了待定系数法求解析式,以及反比例函数和一次函数的交点的求法,熟练掌握待定系数法和解方程是关键.

练习册系列答案
相关题目
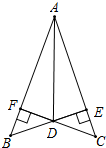 如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于 点D,DE=DF,连结AD.
如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于 点D,DE=DF,连结AD. 如图,PA,PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=70°,则∠P=
如图,PA,PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=70°,则∠P=



 已知:如图,AB=CD,AE=DF,且AE⊥BC于E,DF⊥BC于F.求证:∠B=
已知:如图,AB=CD,AE=DF,且AE⊥BC于E,DF⊥BC于F.求证:∠B=