题目内容
已知:抛物线y=x2-(m-3)x-m
(1)若抛物线的对称轴是直线x=2,求m的值.
(2)若抛物线与x轴负半轴交于两个点,且这两点距离为2
,求m的值.
(3)若抛物线与x轴交于A(x1,0),B(x2,0)两点,与y轴交点为C,∠ACB=90°,试求m的值.
(1)若抛物线的对称轴是直线x=2,求m的值.
(2)若抛物线与x轴负半轴交于两个点,且这两点距离为2
| 6 |
(3)若抛物线与x轴交于A(x1,0),B(x2,0)两点,与y轴交点为C,∠ACB=90°,试求m的值.
考点:抛物线与x轴的交点,二次函数的性质
专题:
分析:(1)根据抛物线的对称轴x=-
建立方程求出其解即可;
(2)设抛物线与x轴负半轴两个交点的横坐标分别为x1,x2(x1<x2),由根与系数的关系建立方程求出其解即可;
(3)由根与系数的关系及勾股定理建立方程求出其解即可.
| b |
| 2a |
(2)设抛物线与x轴负半轴两个交点的横坐标分别为x1,x2(x1<x2),由根与系数的关系建立方程求出其解即可;
(3)由根与系数的关系及勾股定理建立方程求出其解即可.
解答:解:(1)由题意得:
-
=2,
解得:m=7.
答:m的值行为7;
(2)设抛物线与x轴负半轴两个交点的横坐标分别为x1,x2(x1<x2),根据题意,得
x1+x2=m-3,x1x2=-m,x2-x1=2
∵抛物线与x轴的交点在负半轴,
∴x1+x2<0,x1x2>0,
∴
,
∴m<0.
∴(x2-x1)2=24,
∴(x1+x2)2-4x1x2=24,
∴(m-3)2-4(-m)=24,
解得:m1=5(舍去),m2=-3.
答:m=-3;
(3)∵∠ACB=90°
∴AC2+BC2=AB2
当x=0时,y=-m,
∴C(0,-m).
∴x12+m2+x22+m2=(x1-x2)2
2m2=-2x1x2,
∴2m2=2m
解得:m1=0,m2=1.
∵m=0时,A、B、C三点在同一直线上,
∴m的值为1.
-
| -(m-3) |
| 2 |
解得:m=7.
答:m的值行为7;
(2)设抛物线与x轴负半轴两个交点的横坐标分别为x1,x2(x1<x2),根据题意,得
x1+x2=m-3,x1x2=-m,x2-x1=2
| 6 |
∵抛物线与x轴的交点在负半轴,
∴x1+x2<0,x1x2>0,
∴
|
∴m<0.
∴(x2-x1)2=24,
∴(x1+x2)2-4x1x2=24,
∴(m-3)2-4(-m)=24,
解得:m1=5(舍去),m2=-3.
答:m=-3;
(3)∵∠ACB=90°
∴AC2+BC2=AB2
当x=0时,y=-m,
∴C(0,-m).
∴x12+m2+x22+m2=(x1-x2)2
2m2=-2x1x2,
∴2m2=2m
解得:m1=0,m2=1.
∵m=0时,A、B、C三点在同一直线上,
∴m的值为1.
点评:本题考查了抛物线的对称轴的运用,根与系数的关系的运用,一元二次方程的解法的运用,解答时运用二次函数的性质求解是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
数轴上A、B两点分别表示-4
和3,那么A、B两点的距离是( )
| 1 |
| 2 |
A、-1
| ||
B、7
| ||
C、1
| ||
D、-
|

 如图,在等腰Rt△ABC中,∠B=90°.将△ABC绕点A逆时针旋转60°得△AB′C′,则∠AB′C=
如图,在等腰Rt△ABC中,∠B=90°.将△ABC绕点A逆时针旋转60°得△AB′C′,则∠AB′C=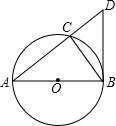 如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D. 如图:直线y1=x+m分别与x轴、y轴交于A、B两点,与双曲线y2=
如图:直线y1=x+m分别与x轴、y轴交于A、B两点,与双曲线y2=