题目内容
12．等腰△ABC中，AB=AC=6，△ABC的面积是12，D是底边BC上任意一点，DE⊥AB于E，DF⊥AC于F，则DE+DF的值为（ ）| A． | 2 | B． | 4 | C． | 8 | D． | 12 |
分析 首先画出几何图形，连接AD，根据三角形的面积公式即可得到$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=12，进而求得DE+DF的值．
解答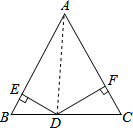 
解：如图所示：连接AD，
∵AB=AC=6，△ABC的面积是12，
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=12，
∴DE+DF=4，
故选B．
点评 本题考查了等腰三角形的性质，三角形的面积，有利于培养同学们钻研和探索问题的精神．
练习册系列答案
相关题目
2．已知函数y=-x2+2x-2-c2（c为常数）的图象上有两点A（x1，y1），B（x2，y2），若x1＜1＜x2且x1+x2＞2，则y1与y2的大小关系是（ ）
| A． | y1＞y2 | B． | y1=y2 | ||
| C． | y1＜y2 | D． | y1与y2的大小不确定 |
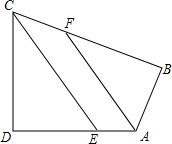如图，四边形ABCD中CD⊥DA，CE平分∠DCB交AD于E，AF平分∠DAB交BC于F，CE∥FA，求∠B．