题目内容
2.已知函数y=-x2+2x-2-c2(c为常数)的图象上有两点A(x1,y1),B(x2,y2),若x1<1<x2且x1+x2>2,则y1与y2的大小关系是( )| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1与y2的大小不确定 |
分析 根据题意可知,函数对称轴为x=1,而由x1+x2>2可知,(x2,y2)位于对称轴的右侧,且距离小于(x1,y1)与对称轴的距离.
解答 解:∵函数y=-x2-2x-2-c2(c为常数)的对称轴为x=-$\frac{2}{2×(-1)}$=1,
根据x1<1<x2可知,A、B两点位于对称轴的两侧,
又∵x1+x2>2,
∴A距离对称轴较远,
可见,y1>y2.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,找到对称轴是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
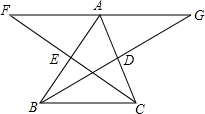 已知:如图,BD、CE为△ABC的两条中线,延长BD到G,使BD=DG,延长CE到F,使CE=EF
已知:如图,BD、CE为△ABC的两条中线,延长BD到G,使BD=DG,延长CE到F,使CE=EF 如图,焊上等长的13根钢条来加固钢架,AP1=P1P2=P2P3=…=P13P14=P13A,则∠A的度数是12°.
如图,焊上等长的13根钢条来加固钢架,AP1=P1P2=P2P3=…=P13P14=P13A,则∠A的度数是12°.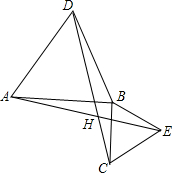 如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
如果两个等边三角形△ABD和△BCE,连接AE与CD,证明: