题目内容
12.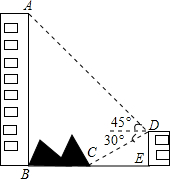 如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.通过解直角△AFD得到DF的长度;通过解直角△DCE得到CE的长度,则BC=BE-CE.
解答  解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.
则DE=BF=CH=10m,
在直角△ADF中,∵AF=80m-10m=70m,∠ADF=45°,
∴DF=AF=70m.
在直角△CDE中,∵DE=10m,∠DCE=30°,
∴CE=$\frac{DE}{tan30°}$=$\frac{10}{\frac{\sqrt{3}}{3}}$=10$\sqrt{3}$(m),
∴BC=BE-CE=70-10$\sqrt{3}$≈70-17.32≈52.7(m).
答:障碍物B,C两点间的距离约为52.7m.
点评 本题考查了解直角三角形-仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
3.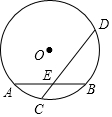 如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
 如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )| A. | 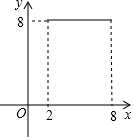 | B. |  | C. | 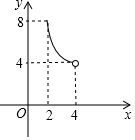 | D. | 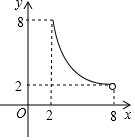 |
7. 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′是( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′是( )
 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′是( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB′是( )| A. | 46° | B. | 45° | C. | 44° | D. | 43° |
 如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.
如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.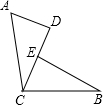 如图,已知∠ACB=90°,且AC=BC,AD⊥CD,BE⊥CD,垂足分别为D、E,求证:CD=BE.
如图,已知∠ACB=90°,且AC=BC,AD⊥CD,BE⊥CD,垂足分别为D、E,求证:CD=BE. 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=60°,∠BCF=45°,这时点F相对于点E升高了4cm.求该摆绳CD的长度.(精确到0.1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)