题目内容
20.在一个不透明的布袋里装有4个标号为-1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小芳从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点(x,y)落在第二象限的概率.
分析 (1)首先根据题意画出表格,即可得到P的所以坐标;
(2)然后由表格求得所有等可能的结果与数字x、y满足点(x,y)落在第二象限的情况,再利用概率公式求解即可求得答案.
解答 解:(1)列表得:
| (x,y) | -1 | 2 | 3 | 4 |
| -1 | (-1,2) | (-1,3) | (-1,4) | |
| 2 | (2,-1) | (2,3) | (2,4) | |
| 3 | (3,-1) | (3,2) | (3,4) | |
| 4 | (4,-1) | (4,2) | (4,3) |
(2)∵共有12种等可能的结果,其中点(x,y)落在第二象限的有3种,
即:(-1,2),(-1,3),(-1,4),
∴点(x,y)落在第二象限的概率为:P=$\frac{3}{12}$=$\frac{1}{4}$.
点评 此题考查的是用列表法或树状图法求概率与不等式的性质.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
11. 如图,A,B,C为⊙O上三点,若∠ACB=20°,则∠BAO的大小为( )
如图,A,B,C为⊙O上三点,若∠ACB=20°,则∠BAO的大小为( )
 如图,A,B,C为⊙O上三点,若∠ACB=20°,则∠BAO的大小为( )
如图,A,B,C为⊙O上三点,若∠ACB=20°,则∠BAO的大小为( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
10.下列计算正确的是( )
| A. | $3\sqrt{15}÷\sqrt{3}=3\sqrt{5}$ | B. | a2×a3=a6 | C. | a2+a=a3 | D. | (-2a2)3=-6a6 |
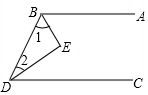
 如图,在菱形ABCD中,对角线AC与BD相交于点O,图中有多少个等腰三角形和直角三角形?
如图,在菱形ABCD中,对角线AC与BD相交于点O,图中有多少个等腰三角形和直角三角形?

 (1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.
(1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.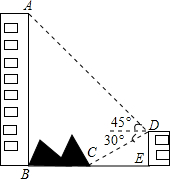 如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼沿右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同-水平直线上.己知AB=80m,DE=10m,求障碍物B、C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)