题目内容
15.在平行四边形ABCD中,已知AB=5,BC=3,则它的周长为16;已知∠A=38°,则∠B=142°,∠C=38°.分析 根据平行四边形的性质可得AB=CD=5,BC=AD=3,进而可得周长;根据平行四边形的性质可得∠A=∠C=38°,AD∥BC,根据平行线的性质可得∠B+∠A=180°,进而可得∠B的度数.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD=5,BC=AD=3,
∴它的周长为:5×2+3×2=16;
∵四边形ABCD是平行四边形,
∴∠A=∠C=38°,AD∥BC,
∴∠B+∠A=180°,
∴∠B=142°,
故答案为:16;142°;38°.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.

练习册系列答案
相关题目
10. 如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
 如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
如图,四边形ABCD中,∠A=90°,AB=$3\sqrt{3}$,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )| A. | 3 | B. | 4 | C. | 4.5 | D. | 5 |
20.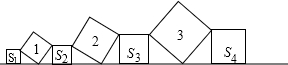 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )| A. | 2500 | B. | 2550 | C. | 2600 | D. | 2800 |
4. 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )| A. | $\frac{12}{25}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
5.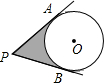 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )| A. | 9$\sqrt{3}$-3π | B. | 9$\sqrt{3}$-2π | C. | $\frac{9}{2}\sqrt{3}-3π$ | D. | $\frac{9}{2}\sqrt{3}-2π$ |
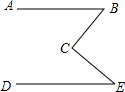 如图,AB∥DE,试问:∠B、∠E、∠BCE有什么关系.
如图,AB∥DE,试问:∠B、∠E、∠BCE有什么关系.