题目内容
11. 如图,在?ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.
如图,在?ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.(1)若∠CFD=55°,求∠BCD的度数;
(2)求证:∠EFC=2∠CFD;
(3)求证:CE⊥AB.
分析 (1)根据平行四边形的性质得出AD∥BC,根据平行线的性质得出∠BCF=∠CFD=55°,求出DF=DC,根据等腰三角形的性质得出∠DCF=∠CFD=55°,即可求出答案;
(2)延长EF和CD交于M,根据平行四边形的性质得出AB∥CD,根据平行线的性质得出∠A=∠FDM,证△EAF≌△MDF,推出EF=MF,求出CF=MF,求出∠M=∠FCD=∠CFD,根据三角形的外角性质求出即可;
(3)求出∠ECD=90°,根据平行线的性质得出∠BEC=∠ECD,即可得出答案.
解答 (1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠CFD=55°,
∴∠BCF=∠CFD=55°,
∵在?ABCD中,AD=2AB,
∴AD=2DC,
∵F为AD的中点,
∴AF=DF,AD=2DF,
∴DF=DC,
∴∠DCF=∠CFD=55°,
∴∠BCD=∠BCF+∠DCF=55°+55°=110°;
(2)证明:延长EF和CD交于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠FDM,
在△EAF和△MDF中,
$\left\{\begin{array}{l}{∠A=∠FDM}\\{AF=DF}\\{∠AFE=∠DFM}\end{array}\right.$,
∴△EAF≌△MDF(ASA),
∴EF=MF,
∵EF=CF,
∴CF=MF,
∴∠FCD=∠M,
∵由(1)知:∠DFC=∠FCD,
∴∠M=∠FCD=∠CFD,
∵∠EFC=∠M+∠FCD=2∠CFD;
(3)解:∵EF=FM=CF,
∴∠ECM=90°,
∵AB∥CD,
∴∠BEC=∠ECM=90°,
∴CE⊥AB.
点评 本题考查了平行四边形的性质,平行线的性质,全等三角形的性质和判定,等腰三角形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键.

 某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:
某食品公司产销一种食品,已知每月的生产成本y1与产量x之间是一次函数关系,函数y1与自变量z(kg)的部分对应值如下表:| x(单位:kg) | 10 | 20 | 30 |
| y1(单位:/元) | 3030 | 3060 | 3090 |
(2)经过试销发现,这种食品每月的销售收入y2(元)与销量x(kg)之间满足如图所示的函数关系
①y2与x之间的函数关系式为Y=5X;
②假设该公司每月生产的该种食品均能全部售出,那么该公司每月至少要生产该种食品多少kg,才不会亏损?
| A. | -3 | B. | -11 | C. | 5 | D. | 11 |
 如图,△ABC在坐标平面内三个顶点的坐标分别为A(1,2)、B(3,3)、C(3,1).
如图,△ABC在坐标平面内三个顶点的坐标分别为A(1,2)、B(3,3)、C(3,1). 如图是一个正方体盒子的表面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字互为相反数.
如图是一个正方体盒子的表面展开图,该正方体六个面上分别标有不同的数字,且相对两个面上的数字互为相反数. 如图,二次函数y=x2-4x+3与坐标轴交于A、B、C三点,C点关于对称轴的对称点为D点,点P在抛物线上,且∠PDB=45°,求P点坐标.
如图,二次函数y=x2-4x+3与坐标轴交于A、B、C三点,C点关于对称轴的对称点为D点,点P在抛物线上,且∠PDB=45°,求P点坐标.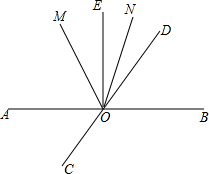 如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.