题目内容
1.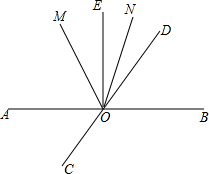 如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.(1)若∠EON=18°,求∠AOC的度数.
(2)试判断∠MON与∠AOE的数量关系,并说明理由.
分析 (1)直接利用角平分线的性质得出∠DOE的度数,再求出∠DOB的度数,进而得出答案;
(2)直接利用未知数表示出∠AOD、∠MOD、∠MON进而求出答案.
解答 解:(1)∵ON平分∠DOE,
∴∠DOE=2∠EON=36°,
∵∠BOE=∠DOE+∠DOB=90°,
∴∠DOB=∠BOE-∠DOE=54°,
∴∠AOC=∠DOB=54°;
(2)∠DON=$\frac{1}{2}$∠AOE
理由:设∠DON=x°,
∵ON平分∠DOE,
∴∠DOE=2∠DON=2x°,
∵∠AOE+∠BOE=180°,∠BOE=90°,
∴∠AOE=180°-∠BOE=90°,
∴∠AOD=∠AOE+∠DOE=(90+2x)°,
∵OM平分∠AOD,
∴∠MOD=$\frac{1}{2}$(90+2x)°=(45+x)°,
∴∠MON=∠MOD-∠DON=45°,
∴∠MON=$\frac{1}{2}$∠AOE=45°.
点评 此题主要考查了角平分线的性质以及垂线定义和邻补角的定义,正确表示出∠AOD的度数是解题关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
12.下列变形正确的是( )
| A. | $\frac{b}{a}=\frac{b^2}{a^2}$ | B. | $\frac{b+1}{a+1}=\frac{b}{a}$ | C. | $\frac{{{a^2}-{b^2}}}{a+b}=a-b$ | D. | $\frac{a}{-a-b}=-\frac{a}{a-b}$ |
9.如果代数式a+b=3,ab=-4,那么代数式3ab-2b-2(ab+a)+1的值等于( )
| A. | -9 | B. | -13 | C. | -21 | D. | -25 |
6.下列等式正确的是( )
| A. | -|-5|=5 | B. | -2(a+3b)=-2a+6b | C. | 3m+2n=5mn | D. | x2y-2x2y=-x2y |
18.下列各图中,射线OA表示南偏东32°方向的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在?ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.
如图,在?ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF. 如图为一块在电脑屏幕上出现的色块图,由6个颜色不同的正方形拼成的长方形,如果中间最小的正方形边长为1,则所拼成的长方形的面积是143.
如图为一块在电脑屏幕上出现的色块图,由6个颜色不同的正方形拼成的长方形,如果中间最小的正方形边长为1,则所拼成的长方形的面积是143. 如图,抛物线y=ax2+2ax+c(a>0)与x轴交于A(-3,0)、B两点(A在B的左侧),与y轴交于点C(0,-3),抛物线的顶点为M.
如图,抛物线y=ax2+2ax+c(a>0)与x轴交于A(-3,0)、B两点(A在B的左侧),与y轴交于点C(0,-3),抛物线的顶点为M.