题目内容
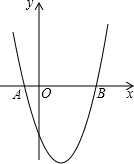 如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,直线y=kx-1与抛物线交于P、Q两点,且y轴平分线段PQ,求k的值.考点:抛物线与x轴的交点
专题:
分析:由直线方程和抛物线方程得到x2-2x-3=kx-1,利用线段PQ的中点的横坐标是0,结合韦达定理可以求得k的值.
解答:解:∵抛物线y=x2-2x-3与直线y=kx-1交于P、Q两点,
∴x2-2x-3=kx-1,
整理,得x2-(2+k)x-2=0,
设P(x1,y1),Q(x2,y2),则x1+x2=2+k.
∵y轴平分线段PQ,
∴线段PQ的中点的横坐标是0,即
=
=0,
解得 k=-2.
即k的值是-2.
∴x2-2x-3=kx-1,
整理,得x2-(2+k)x-2=0,
设P(x1,y1),Q(x2,y2),则x1+x2=2+k.
∵y轴平分线段PQ,
∴线段PQ的中点的横坐标是0,即
| x1+x2 |
| 2 |
| 2+k |
| 2 |
解得 k=-2.
即k的值是-2.
点评:本题考查了抛物线与x轴的交点.解题时要从题干的信息“y轴平分线段PQ”中挖掘出已知条件:线段PQ的中点的横坐标是0.

练习册系列答案
相关题目
如果(a+3)2+|b-2|=0,那么代数式(a+b)2015的值是( )
| A、-2015 | B、2015 |
| C、1 | D、-1 |
2013×2013-2013×2012-2011×2012+2012×2012的值是( )
| A、1 | B、-1 |
| C、4025 | D、4024 |
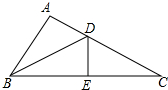 已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.
已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.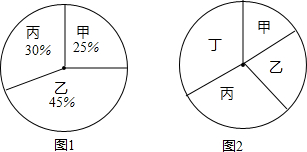 分别求出每个扇形的圆心角的度数.
分别求出每个扇形的圆心角的度数.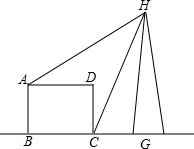 如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m).
如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m). (1)如图,在锐角△ABC中,利用三角函数的定义及勾股定理证明你的猜想;
(1)如图,在锐角△ABC中,利用三角函数的定义及勾股定理证明你的猜想;