题目内容
 如图,MA、MB是⊙O的切线,切点分别为A、B,若∠ACB=65°,则∠AMB=
如图,MA、MB是⊙O的切线,切点分别为A、B,若∠ACB=65°,则∠AMB=考点:切线的性质
专题:
分析:首先连接OA,OB,由MA、MB是⊙O的切线,即可得∠MAO=∠MBO=90°,又由∠ACB=65°,即可求得∠AOB的度数,然后由四边形内角和定理即可求得答案.
解答: 解:连接OA,OB,
解:连接OA,OB,
∵MA、MB是⊙O的切线,
∴∠MAO=∠MBO=90°,
∵∠ACB=65°,
∴∠AOB=2∠ACB=130°,
∴∠AMB=360°-∠AOB-∠MAO-∠MBO=50°.
故答案是:50.
 解:连接OA,OB,
解:连接OA,OB,∵MA、MB是⊙O的切线,
∴∠MAO=∠MBO=90°,
∵∠ACB=65°,
∴∠AOB=2∠ACB=130°,
∴∠AMB=360°-∠AOB-∠MAO-∠MBO=50°.
故答案是:50.
点评:此题考查了切线的性质与圆周角定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
| A、若a、b、c是△ABC的三边,则a2+b2=c2 |
| B、若a、b、c是Rt△ABC的三边,∠B=90°,则a2+b2=c2 |
| C、若a、b、c是Rt△ABC的三边,∠A=90°,则a2+b2=c2 |
| D、若a、b、c是Rt△ABC的三边,∠C=90°,则a2+b2=c2 |
三角形的外心是( )
| A、各内角的平分线的交点 |
| B、各边中线的交点 |
| C、各边垂线的交点 |
| D、各边垂直平分线的交点 |
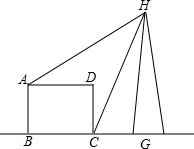 如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m).
如图所示,形状为长方形的建筑物ABCD的底端BC的长是70cm,高AB=30m,从A,C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°,求塔的高度HG(精确到1m). 已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).
已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).