题目内容
15.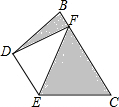 DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )
DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
分析 根据折叠的性质得到△DEF的面积,再根据三角形的中位线定理,结合相似三角形的性质可以求得△ABC的面积,从而求解.
解答 解:∵DE是△ABC的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC.
∴△ADE∽△ABC.
∴$\frac{S△ADE}{S△ABC}=\frac{1}{4}$.
∵△DEF的面积为3,
∴△ADE的面积为3,
∴△ABC的面积=12.
∴图中阴影部分的面积为12-3-3=6.
故选:B.
点评 此题综合考查了翻折变换(折叠问题)、三角形的中位线定理和相似三角形的判定和性质.关键是掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
4.若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若十位上数字为7,则从3、4、5、6、8、9中任选两数,与7组成“中高数”的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
 某工厂在长方形材料上截取圆形配件,如图,求此材料的利用率(圆形配件的总面积与材料面积的比,结果精确到1%,截取过程中不计损耗).
某工厂在长方形材料上截取圆形配件,如图,求此材料的利用率(圆形配件的总面积与材料面积的比,结果精确到1%,截取过程中不计损耗).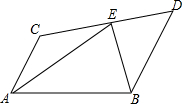 如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件:
如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件: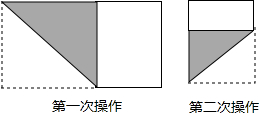
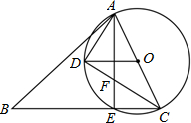 如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE、AD、DC.
如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE、AD、DC.