题目内容
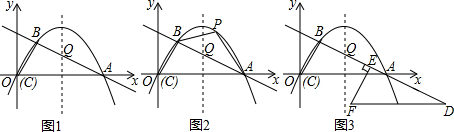
3.若抛物线y=ax2+bx+c上有两点A,B关于原点对称,则称它为“完美抛物线”.(1)请猜猜看:抛物线y=x2+x-1是否是“完美抛物线”?若猜是,请写出A,B坐标,若不是,请说明理由;
(2)若抛物线y=ax2+bx+c是“完美抛物线”与y轴交于点C,与x轴交于(-$\frac{c}{2}$,0),若S△ABC=$\frac{{c}^{2}}{b}$,求直线AB解析式.
分析 (1)首先设A点的坐标是(m,n),根据A,B关于原点对称,判断出B点的坐标是(-m,-n);然后根据A,B都是抛物线y=x2+x-1上的点,求出m、n的值各是多少,判断出抛物线y=x2+x-1是“完美抛物线”,并写出A,B坐标即可.
(2)首先根据抛物线y=ax2+bx+c上有两点A,B关于原点对称,可得直线AB经过原点,设直线AB解析式是:y=kx;设点A的坐标是(p,q),则B点的坐标是(-p,-q);然后根据A、B都是抛物线y=x2+x-1上的点,抛物线与x轴交于(-$\frac{c}{2}$,0),可得2b-ac=4;最后根据S△ABC=$\frac{{c}^{2}}{b}$,求出b的值是多少,进而判断出直线AB的斜率是多少,求出直线AB解析式即可.
解答 解:(1)设A点的坐标是(m,n),
∵A,B关于原点对称,
∴B点的坐标是(-m,-n),
∵A,B都是抛物线y=x2+x-1上的点,
∴$\left\{\begin{array}{l}{{m}^{2}+m-1=n…①}\\{{(-m)}^{2}-m-1=-n…②}\end{array}\right.$,
解得m=1或m=-1,
①当m=1时,
n=12+1-1=1,
②当m=-1时,
n=(-1)2-1-1=-1,
∴抛物线y=x2+x-1是“完美抛物线”,
A(1,1)、B(-1,-1)或A(-1,-1)、B(1,1).
(2)∵抛物线y=ax2+bx+c上有两点A,B关于原点对称,
∴直线AB经过原点,
∴设直线AB解析式是:y=kx,
设点A的坐标是(p,q),
则B点的坐标是(-p,-q),
∴$\left\{\begin{array}{l}{{ap}^{2}+bp+c=q}\\{a{•(-p)}^{2}+b•(-p)+c=-q}\end{array}\right.$,
∴ap2+c=0,
∴bp=q,
∴${p}^{2}=-\frac{c}{a}$,
∵抛物线y=ax2+bx+c与x轴交于(-$\frac{c}{2}$,0),
∴$a{•(-\frac{c}{2})}^{2}+b•(-\frac{c}{2})+c=0$,
∴2b-ac=4,
∵点C的坐标是(0,c),
∴|$\frac{1}{2}$cp×2|=$\frac{{c}^{2}}{b}$,
∴${{c}^{2}p}^{2}=\frac{{c}^{4}}{{b}^{2}}$,
∴p2=$\frac{{c}^{2}}{{b}^{2}}$,
又∵${p}^{2}=-\frac{c}{a}$,
∴$\frac{{c}^{2}}{{b}^{2}}=-\frac{c}{a}$,
∴b2=-ac,
又∵2b-ac=4,
∴b2+2b-4=0,
∴b=-1$±\sqrt{5}$,
∵S△ABC=$\frac{{c}^{2}}{b}$>0,
∴b>0,
∴b=$\sqrt{5}$-1,
又∵bp=q,
∴$\frac{q}{p}=b=\sqrt{5}-1$,
即直线AB的斜率是:k=$\sqrt{5}-1$,
∴直线AB解析式是:y=($\sqrt{5}$-1)x.
点评 (1)此题主要考查了二次函数图象上点的坐标的特征,以及对“完美抛物线”的含义的理解,要熟练掌握.
(2)此题还考查了直线的解析式的求法,要熟练掌握,解答此题的关键是求出直线AB的斜率是多少.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
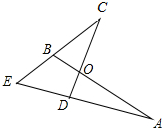 如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC.你能证明∠A=∠C吗?点O在∠AEC的平分线上吗?
如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC.你能证明∠A=∠C吗?点O在∠AEC的平分线上吗?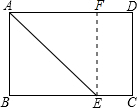 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.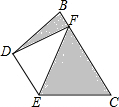 DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )
DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )