题目内容
7.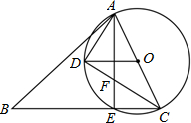 如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE、AD、DC.
如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,$\frac{1}{2}$AC长为半径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE、AD、DC.(1)求证:D是$\widehat{AE}$的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若$\frac{{S}_{△CEF}}{{S}_{△OCD}}$=$\frac{1}{2}$,且AC=6,求CF的长.
分析 (1)根据圆周角定理,由AC为直径得到∠AEC=90°,由于OD∥BC,根据平行线的性质得OD⊥AE,则根据垂径定理得$\widehat{AD}$=$\widehat{DE}$;
(2)延长DO交AB于G点,如图,根据平行线性质得∠OGA=∠B,再利用三角形外角性质有∠ODA=∠DGA+∠GAD,加上∠DAO=∠ODA,于是得到∠DAO=∠B+∠BAD;
(3)作OH⊥CD于H,如图,根据垂径定理得到CH=DH,则利用三角形面积公式得S△OCH=$\frac{1}{2}$S△ODC,由$\frac{{S}_{△CEF}}{{S}_{△OCD}}$=$\frac{1}{2}$得S△OCH=S△CEF,再根据圆周角定理,由$\widehat{AD}$=$\widehat{DE}$得到∠ACD=∠ECD,于是可判断Rt△CEF∽Rt△CHO,根据相似三角形的性质得$\frac{{S}_{△CEF}}{{S}_{△CHO}}$=($\frac{CF}{CO}$)2=1,所以CF=CO=3.
解答 (1)证明:∵AC为直径,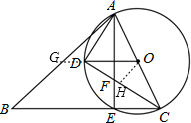
∴∠AEC=90°,
∴AE⊥BC,
∵OD∥BC,
∴OD⊥AE,
∴$\widehat{AD}$=$\widehat{DE}$,
∴D是$\widehat{AE}$的中点;
(2)证明:延长DO交AB于G点,如图,
∵OG∥BC,
∴∠OGA=∠B,
∵∠ODA=∠DGA+∠GAD,
∴∠ODA=∠B+∠BAD,
∵OA=OD,
∴∠DAO=∠ODA,
∴∠DAO=∠B+∠BAD;
(3)解:作OH⊥CD于H,如图,则CH=DH,
∴S△OCH=$\frac{1}{2}$S△ODC,
∵$\frac{{S}_{△CEF}}{{S}_{△OCD}}$=$\frac{1}{2}$,
∴S△OCH=S△CEF,
∵$\widehat{AD}$=$\widehat{DE}$,
∴∠ACD=∠ECD,
∴Rt△CEF∽Rt△CHO,
∴$\frac{{S}_{△CEF}}{{S}_{△CHO}}$=($\frac{CF}{CO}$)2=1,
∴CF=CO=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3.
点评 本题考查了圆的综合题:熟练掌握平行线的性质、垂径定理和圆周角定理;会运用相似三角形的判定与性质判断线段之间的关系.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | -1 | B. | 1 | C. | 5 | D. | -5 |
 甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).
甲从M地出发去N地,乙搭甲的便车也从M地出发到途中与M,N两地在同一条直线上的G地.甲在N地停留一段时间后以110km/h的速度返回,乙在G地停留了$\frac{3}{4}$h后,徒步返回M地,走了5km时与返回的甲相遇并搭甲车返回M地.如图是两人与M地的距离y(单位:km)与行进时间x(单位:h)之间的函数图象(甲、乙均匀速行进,不考虑其他因素).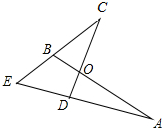 如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC.你能证明∠A=∠C吗?点O在∠AEC的平分线上吗?
如图,AB交CD于点O,AD、CB的延长线相交于点E,且OA=OC,EA=EC.你能证明∠A=∠C吗?点O在∠AEC的平分线上吗?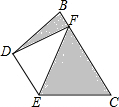 DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )
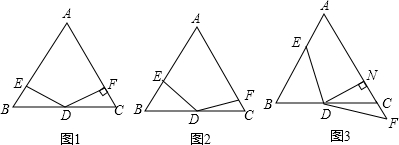
DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )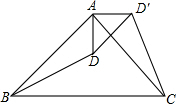 如图,△ABC是等腰直角三角形,BC是斜边,将△ABD绕点A逆时针旋转后,能与△ACD′重合.如果AD=2,那么DD′=2$\sqrt{2}$.
如图,△ABC是等腰直角三角形,BC是斜边,将△ABD绕点A逆时针旋转后,能与△ACD′重合.如果AD=2,那么DD′=2$\sqrt{2}$.