题目内容
5.解不等式:$\frac{2x-1}{3}$≤$\frac{3x+2}{4}$-1,并把解集表示在数轴上.分析 先去分母,再去括号,移项、合并同类项,把x的系数化为1即可.
解答 解:去分母得,4(2x-1)≤3(3x+2)-12,
去括号得,8x-4≤9x+6-12,
移项得,8x-9x≤6-12+4,
合并同类项得,-x≤-2,
把x的系数化为1得,x≥2.
在数轴上表示为: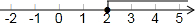 .
.
点评 本题考查的是解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.-2的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
10.若反比例函数y=$\frac{k}{x}$的图象经过点(2,-1),则该反比例函数的图象在( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
14.下列y关于x的函数中,是正比例函数的为( )
| A. | y=x2 | B. | y=$\frac{2}{x}$ | C. | y=$\frac{x}{2}$ | D. | y=$\frac{x+1}{2}$ |
15.四个数-3.14,0,1,2中为负数的是( )
| A. | -3.14 | B. | 0 | C. | 1 | D. | 2 |
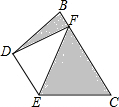 DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )
DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )