题目内容
6.如图,在矩形AOCD,顶点A(0,4),顶点C(5,0).动点P从点O出发,沿线段OA的方向以每秒1个单位长的速度运动,动点E从点A出发,沿着折线AD-DC以每秒2个单位的速度向点C运动,点P,E分别从点O,A同时出发,当点P运动到点A时,点E随之停止运动,设运动时间为t(秒).求:(1)矩形AOCD的顶点D坐标;
(2)当点P到达点A时,求点E的坐标;
(3)当t为何值时,四边形PADE是矩形?
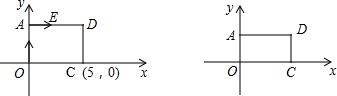
分析 (1)根据矩形的性质得到AO=CD,AD=OC,由A(0,4),C(5,0),即可得到结论;
(2)当点P到达点A时,求得t=$\frac{OA}{1}$=4,于是得到点E所走的路程=2×4=8,即可得到结果;
(3)当四边形PADE是矩形,这时E在CD上,根据矩形的性质列方程即可得到结果.
解答 解:(1)∵在矩形AOCD中,
∴AO=CD,AD=OC,
∵A(0,4),C(5,0),
∴CD=4,AD=5,
∴D(5,4);
(2)当点P到达点A时,
∵t=$\frac{OA}{1}$=4,
∴点E所走的路程=2×4=8,
∴点E在CD上,
∴CE=9-8=1,
∴E(5,1);
(3)当四边形PADE是矩形,这时E在CD上,
∴DE=2t-5,AP=4-t,
根据题意:AP=DE,
即:4-t=2t-5,
解得:t=3,
∴当t=3时,四边形PADE是矩形.
点评 本题考查了坐标与图形的性质,矩形的判定和性质,动点问题,熟练掌握矩形的性质是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
18.下列方程中,一元二次方程是( )
| A. | ${x^2}+\frac{1}{x^2}=4$ | B. | ax2+bx-3=0 | C. | (x-1)(x+2)=1 | D. | 3x2-2xy-5y2=0 |
15. 如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )
如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )
 如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )
如图,△ABC中,∠B=90°,D为BC上的一点,若∠ADC=6x°,则x可能为( )| A. | 5 | B. | 15 | C. | 25 | D. | 35 |
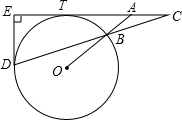 如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.
如图,已知等腰三角形ABC,AB=AC,O为AB延长线上的点,以⊙O为圆心,OB为半径作O,交CB的延长线于D,⊙O与直线AC切于点T,作DE⊥AC,垂足为E.